MultilayerGraphs.jl
MultilayerGraphs.jl: Multilayer Network Science in Julia - Published in JOSS (2023)
Science Score: 98.0%
This score indicates how likely this project is to be science-related based on various indicators:
-
✓CITATION.cff file
Found CITATION.cff file -
✓codemeta.json file
Found codemeta.json file -
✓.zenodo.json file
Found .zenodo.json file -
✓DOI references
Found 77 DOI reference(s) in README and JOSS metadata -
✓Academic publication links
Links to: joss.theoj.org, zenodo.org -
○Committers with academic emails
-
○Institutional organization owner
-
✓JOSS paper metadata
Published in Journal of Open Source Software
Keywords
Keywords from Contributors
Repository
A Julia package for the creation, manipulation and analysis of the structure, dynamics and functions of multilayer graphs.
Basic Info
- Host: GitHub
- Owner: JuliaGraphs
- License: mit
- Language: Julia
- Default Branch: main
- Homepage: https://juliagraphs.org/MultilayerGraphs.jl/dev
- Size: 14.3 MB
Statistics
- Stars: 123
- Watchers: 10
- Forks: 5
- Open Issues: 36
- Releases: 10
Topics
Metadata Files
README.md
MultilayerGraphs.jl
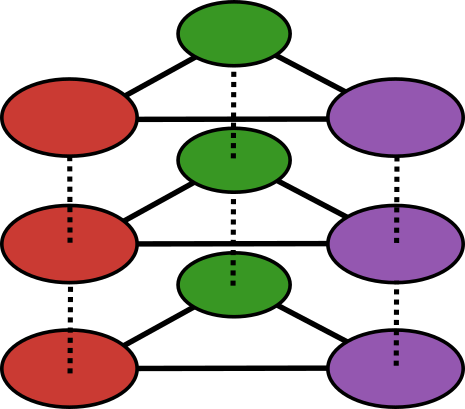
MultilayerGraphs.jl is a Julia package for the creation, manipulation and analysis of the structure, dynamics and functions of multilayer graphs.
🌐 Overview
A multilayer graph is a graph consisting of multiple standard subgraphs called layers which can be interconnected through bipartite graphs called interlayers composed of the vertex sets of two different layers and the edges between them. The vertices in each layer represent a single set of nodes, although not all nodes have to be represented in every layer.
Formally, a multilayer graph can be defined as a triple $G=(V,E,L)$, where:
- $V$ is the set of vertices;
- $E$ is the set of edges, pairs of nodes $(u, v)$ representing a connection, relationship or interaction between the nodes $u$ and $v$;
- $L$ is a set of layers, which are subsets of $V$ and $E$ encoding the nodes and edges within each layer.
Each layer $\ell$ in $L$ is a tuple $(V\ell, E\ell)$, where $V\ell$ is a subset of $V$ that represents the vertices within that layer, and $E\ell$ is a subset of $E$ that represents the edges within that layer.
Multiple theoretical frameworks have been proposed to formally subsume all instances of multilayer graphs (De Domenico et al. (2013); Kivelä et al. (2014); Boccaletti et al. (2014); Lee et al. (2015); Aleta and Moreno (2019); Bianconi (2018); Cozzo et al. (2018); Artime et al. (2022); De Domenico (2022)).
Multilayer graphs have been adopted to model the structure and dynamics of a wide spectrum of high-dimensional, non-linear, multi-scale, time-dependent complex systems including physical, chemical, biological, neuronal, socio-technical, epidemiological, ecological and economic networks (Cozzo et al. (2013); Granell et al. (2013); Massaro and Bagnoli (2014); Estrada and Gomez-Gardenes (2014); Azimi-Tafreshi (2016); Baggio et al. (2016); DeDomenico et al. (2016); Amato et al. (2017); DeDomenico (2017); Pilosof et al. (2017); de Arruda et al. (2017); Gosak et al. (2018); Soriano-Panos et al. (2018); Timteo et al. (2018); Buldú et al. (2018); Lim et al. (2019); Mangioni et al. (2020); Aleta et al. (2020); Aleta et al. (2022)).
MultilayerGraphs.jl is an integral part of the JuliaGraphs ecosystem extending Graphs.jl so all the methods and metrics exported by Graphs.jl work for multilayer graphs, but due to the special nature of multilayer graphs the package features a peculiar implementation that maps a standard integer-labelled vertex representation to a more user-friendly framework exporting all the objects an experienced practitioner would expect such as nodes (Node), vertices (MultilayerVertex), layers (Layer), interlayers (Interlayer), etc.
MultilayerGraphs.jl features multilayer-specific methods and metrics including the global clustering coefficient, the overlay clustering coefficient, the multilayer eigenvector centrality, the multilayer modularity and the Von Neumann entropy.
Finally, MultilayerGraphs.jl has been integrated within the JuliaDynamics ecosystem so that any Multilayer(Di)Graph can be utilised as an argument to the GraphSpace constructor in Agents.jl.
🔰 Installation
To install the latest stable release of MultilayerGraphs.jl, make sure you have installed Julia v1.8 or later and run the following command:
julia
using Pkg
Pkg.add("MultilayerGraphs")
The development version can be installed as follows:
julia
using Pkg
Pkg.add(url="https://github.com/JuliaGraphs/MultilayerGraphs.jl")
🔍 Usage
Let's begin by importing the necessary dependencies and setting the relevant constants.
```julia
Import necessary dependencies
using Distributions, Graphs, SimpleValueGraphs using MultilayerGraphs
Set the number of nodes
const n_nodes = 100
Create a list of nodes
const nodelist = [Node("node$i") for i in 1:n_nodes] ```
Layers and Interlayers
We will instantiate layers and interlayers with randomly-selected edges and vertices adopting a variety of techniques. Layers and Interlayers are not immutable, and mostly behave like normal graphs. The user is invited to consult the API for further details.
Here we define a layer with an underlying simple directed graph using a graph generator-like (or "configuration model"-like) constructor which allows us to specify both the indegree and the outdegree sequences. Before instantiating each layer we sample the number of its vertices and, optionally, of its edges.
```julia
Create a simple directed layer
nvertices = rand(1:100) # Number of vertices layersimpledirected = layersimpledigraph( # Layer constructor :layersimpledirected, # Layer name sample(nodelist, nvertices; replace=false), # Nodes represented in the layer Truncated(Normal(5, 5), 0, 20), # Indegree sequence distribution Truncated(Normal(5, 5), 0, 20) # Outdegree sequence distribution ) ```
Then we define a layer with an underlying simple weighted directed graph. This is another kind of constructor that allows the user to specify the number of edges to be randomly distributed among vertices.
```julia
Create a simple directed weighted layer
nvertices = rand(1:nnodes) # Number of vertices nedges = rand(nvertices:(nvertices * (nvertices - 1) - 1)) # Number of edges layersimpledirectedweighted = layersimpleweighteddigraph( # Layer constructor :layersimpledirectedweighted, # Layer name sample(nodelist, nvertices; replace=false), # Nodes represented in the layer nedges; # Number of randomly distributed edges defaultedgeweight=(src, dst) -> rand() # Function assigning weights to edges ) ```
Similar constructors, more flexible at the cost of ease of use, enable a finer tuning. The constructor we use below should be necessary only in rare circumstances, e.g. if the equivalent simplified constructor layer_simplevaldigraph is not able to infer the correct return types of default_vertex_metadata or default_edge_metadata, or to use and underlying graph structure that isn't currently supported.
```julia
Create a simple directed value layer
nvertices = rand(1:nnodes) # Number of vertices
nedges = rand(nvertices:(nvertices * (nvertices - 1) - 1)) # Number of edges
defaultvertexmetadata = v -> ("vertex$(v)metadata",) # Vertex metadata
defaultedgemetadata = (s, d) -> (rand(),) # Edge metadata
layersimpledirectedvalue = Layer( # Layer constructor
:layersimpledirectedvalue, # Layer name
sample(nodelist, nvertices; replace=false), # Nodes represented in the layer
nedges, # Number of randomly distributed edges
ValDiGraph(
SimpleDiGraph{Int64}();
vertexvaltypes=(String,),
vertexvalinit=defaultvertexmetadata,
edgevaltypes=(Float64,),
edgevalinit=defaultedgemetadata,
),
Float64;
defaultvertexmetadata=defaultvertexmetadata, # Vertex metadata
defaultedgemetadata=defaultedge_metadata # Edge metadata
)
Create a list of layers
layers = [layersimpledirected, layersimpledirectedweighted, layersimpledirectedvalue] ```
There are many more constructors the user is encouraged to explore in the package documentation.
The interface of interlayers is very similar to that of layers. It is very important to notice that, in order to define a Multilayer(Di)Graph, interlayers don't need to be explicitly constructed by the user since they are automatically identified by the Multilayer(Di)Graph constructor, but for more complex interlayers the manual instantiation is required.
Here we define an interlayer with an underlying simple directed graph.
```julia
Create a simple directed interlayer
nvertices1 = nv(layersimpledirected) # Number of vertices of layer 1 nvertices2 = nv(layersimpledirectedweighted) # Number of vertices of layer 2 nedges = rand(1:(nvertices1 * nvertices2 - 1)) # Number of interlayer edges interlayersimpledirected = interlayersimpledigraph( # Interlayer constructor layersimpledirected, # Layer 1 layersimpledirectedweighted, # Layer 2 n_edges # Number of edges ) ```
The interlayer exports a more flexible constructor too.
```julia
Create a simple directed meta interlayer
nvertices1 = nv(layersimpledirectedweighted) # Number of vertices of layer 1 nvertices2 = nv(layersimpledirectedvalue) # Number of vertices of layer 2 nedges = rand(1:(nvertices1 * nvertices2 - 1)) # Number of interlayer edges interlayersimpledirectedmeta = interlayermetadigraph( # Interlayer constructor layersimpledirectedweighted, # Layer 1 layersimpledirectedvalue, # Layer 2 nedges; # Number of edges defaultedgemetadata=(src, dst) -> # Edge metadata (edgemetadata="metadataofedgefrom$(src)to$(dst)",), transfervertex_metadata=true # Boolean deciding layer vertex metadata inheritance )
Create a list of interlayers
interlayers = [interlayersimpledirected, interlayersimpledirected_meta] ```
Multilayer Graphs
Let's construct a directed multilayer graph (MultilayerDiGraph).
```julia
Create a simple directed multilayer graph
multilayerdigraph = MultilayerDiGraph( # Constructor layers, # The (ordered) collection of layers interlayers; # The manually specified interlayers # The interlayers that are left unspecified # will be automatically inserted according # to the keyword argument below defaultinterlayersstructure="multiplex" # The automatically specified interlayers will have only diagonal couplings )
Layers and interlayer can be accessed as properties using their names
multilayerdigraph.layersimpledirected_value ```
Then we proceed by showing how to add nodes, vertices and edges to a directed multilayer graph. The user may add vertices that do or do not represent nodes which are already present in the multilayer graph. In the latter case, we have to create a node first and then add the vertex representing such node to the multilayer graph. The vertex-level metadata are effectively considered only if the graph underlying the relevant layer or interlayer supports them, otherwise they are discarded. The same holds for edge-level metadata and/or weight.
```julia
Create a node
newnode1 = Node("newnode1")
Add the node to the multilayer graph
addnode!(multilayerdigraph, newnode_1)
Create a vertex representing the node
newvertex1 = MV( # Constructor (alias for "MultilayerVertex") newnode1, # Node represented by the vertex :layersimpledirectedvalue, # Layer containing the vertex ("newmetadata",) # Vertex metadata )
Add the vertex
addvertex!( multilayerdigraph, # MultilayerDiGraph the vertex will be added to newvertex_1 # MultilayerVertex to add )
Create another node in another layer
newnode2 = Node("newnode2")
Create another vertex representing the new node
newvertex2 = MV(newnode2, :layersimpledirected_value)
Add the new vertex
addvertex!( multilayerdigraph, newvertex2; addnode=true # Add the associated node before adding the vertex )
Create an edge
newedge = MultilayerEdge( # Constructor newvertex1, # Source vertex newvertex2, # Destination vertex ("someedge_metadata",) # Edge metadata )
Add the edge
addedge!( multilayerdigraph, # MultilayerDiGraph the edge will be added to newedge # MultilayerVertex to add ) ```
Finally we illustrate how to compute a few multilayer metrics such as the global clustering coefficient, the overlay clustering coefficient, the multilayer eigenvector centrality, and the multilayer modularity as defined in De Domenico et al. (2013).
```julia
Compute the global clustering coefficient
multilayerglobalclustering_coefficient(multilayerdigraph)
Compute the overlay clustering coefficient
overlayclusteringcoefficient(multilayerdigraph)
Compute the multilayer eigenvector centrality
eigenvector_centrality(multilayerdigraph)
Compute the multilayer modularity
modularity( multilayerdigraph, rand([1, 2, 3, 4], length(nodes(multilayerdigraph)), length(multilayerdigraph.layers)) ) ```
🎯 Future Developments
All the information regarding the future developments of MultilayerGraphs.jl can be found in the issues.
🛠 How to Contribute
The ongoing development of this package would greatly benefit from the valuable feedback of the esteemed members of the JuliaGraph community, as well as from graph theorists, network scientists, and any users who may have general questions or suggestions.
We therefore encourage you to participate in discussions, raise issues, or submit pull requests. Your contributions are welcome!
🎓 How to Cite
If you utilize this package in your project, please consider citing this repository using the citation information provided in CITATION.bib.
This will help to give appropriate credit to the contributors and support the continued development of the package.
📢 Announcements
v0.1
MultilayerGraphs.jl (v0.1) and its features were announced on the following platforms:
v1.1
MultilayerGraphs.jl (v1.1) and its features were announced on the following platforms:
📹 Talks
18th Workshop on Algorithms and Models for Web Graphs
- When: 2023/05/23 - 2023/05/26
- Where: The Fields Institute, Toronto, Canada
- Who: Pietro Monticone and Claudio Moroni
- What: "Multilayer Network Science in Julia with
MultilayerGraphs.jl" (Website, Slides, Video)
JuliaCon 2023
- When: 2023/07/25 - 2023/07/29
- Where: Massachusetts Institute of Technology, Cambridge, MA, USA
- Who: Pietro Monticone and Claudio Moroni
- What: "
MultilayerGraphs.jl: Multilayer Network Science in Julia" (Website, Short Presentation, Long Presentation, Video)
📦 Related Packages
R
Here is a list of software packages for the creation, manipulation, analysis and visualisation of multilayer graphs implemented in the R language:
muxVizimplements functions to perform multilayer correlation analysis, multilayer centrality analysis, multilayer community structure detection, multilayer structural reducibility, multilayer motifs analysis and utilities to statically and dynamically visualise multilayer graphs;multinetimplements functions to import, export, create and manipulate multilayer graphs, several state-of-the-art multiplex graph analysis algorithms for centrality measures, layer comparison, community detection and visualization;mullyimplements functions to import, export, create, manipulate and merge multilayer graphs and utilities to visualise multilayer graphs in 2D and 3D;multinetsimplements functions to import, export, create, manipulate multilayer graphs and utilities to visualise multilayer graphs.
Python
Here is a list of software packages for the creation, manipulation, analysis and visualisation of multilayer graphs implemented in the Python language:
MultiNetXimplements methods to create undirected networks with weighted or unweighted links, to analyse the spectral properties of adjacency or Laplacian matrices and to visualise multilayer graphs and dynamical processes by coloring the nodes and links accordingly;PyMNetimplements data structures for multilayer graphs and multiplex graphs, methods to import, export, create, manipulate multilayer graphs and for the rule-based generation and lazy-evaluation of coupling edges and utilities to visualise multilayer graphs.
Julia
At the best of our knowledge there are currently no software packages dedicated to the creation, manipulation and analysis of multilayer graphs implemented in the Julia language apart from MultilayerGraphs.jl itself.
📚 References
- De Domenico et al. (2013) Mathematical Formulation of Multilayer Networks. Physical Review X;
- Kivelä et al. (2014) Multilayer networks. Journal of Complex Networks;
- Boccaletti et al. (2014) The structure and dynamics of multilayer networks. Physics Reports;
- Lee et al. (2015) Towards real-world complexity: an introduction to multiplex networks. The European Physical Journal B;
- Bianconi (2018) Multilayer Networks: Structure and Function. Oxford University Press;
- Cozzo et al. (2018) Multiplex Networks: Basic Formalism and Structural Properties. SpringerBriefs in Complexity;
- Aleta and Moreno (2019) Multilayer Networks in a Nutshell. Annual Review of Condensed Matter Physics;
- Artime et al. (2022) Multilayer Network Science: From Cells to Societies. Cambridge University Press;
- De Domenico (2022) Multilayer Networks: Analysis and Visualization. Springer Cham.
- De Domenico (2023) More is different in real-world multilayer networks. Nature Physics
Owner
- Name: JuliaGraphs
- Login: JuliaGraphs
- Kind: organization
- Website: https://juliagraphs.org
- Repositories: 34
- Profile: https://github.com/JuliaGraphs
Graph modeling and analysis packages for the Julia programming language
JOSS Publication
MultilayerGraphs.jl: Multilayer Network Science in Julia
Authors
Tags
Graphs Networks Complexity Complex-Networks Complex-Systems Network-Science Network-Analysis Multilayer-Graphs Multilayer-NetworksCitation (CITATION.bib)
@software{Moroni_Monticone_MultilayerGraphs_2022,
abstract = {A Julia package for the creation, manipulation and analysis of the structure, dynamics and functions of multilayer graphs.},
author = {Moroni, Claudio and Monticone, Pietro},
doi = {10.5281/zenodo.7009172},
institution = {University of Turin (UniTO)},
keywords = {Julia Language, Julia Package, Graph Theory, Applied Graph Theory, Network Theory, Network Science, Graphs, Multilayer Graphs, Multilevel Graphs, Hierarchical Graphs, Networks, Multilayer Networks, Multilevel Networks, Hierarchical Networks, Complexity, Complex Systems},
license = {MIT},
organization = {Interdisciplinary Physics Team (InPhyT)},
title = {MultilayerGraphs.jl},
url = {https://doi.org/10.5281/zenodo.7009172},
year = {2022}
}
GitHub Events
Total
- Issues event: 1
- Watch event: 2
- Issue comment event: 3
- Pull request event: 6
- Fork event: 2
- Create event: 3
Last Year
- Issues event: 1
- Watch event: 2
- Issue comment event: 3
- Pull request event: 6
- Fork event: 2
- Create event: 3
Committers
Last synced: 7 months ago
Top Committers
| Name | Commits | |
|---|---|---|
| Interdisciplinary Physics Team (InPhyT) | 6****m | 234 |
| github-actions[bot] | 4****] | 11 |
| Pietro Monticone | 3****e | 3 |
Issues and Pull Requests
Last synced: 6 months ago
All Time
- Total issues: 33
- Total pull requests: 82
- Average time to close issues: 29 days
- Average time to close pull requests: about 15 hours
- Total issue authors: 8
- Total pull request authors: 7
- Average comments per issue: 0.67
- Average comments per pull request: 0.37
- Merged pull requests: 64
- Bot issues: 0
- Bot pull requests: 16
Past Year
- Issues: 1
- Pull requests: 7
- Average time to close issues: N/A
- Average time to close pull requests: N/A
- Issue authors: 1
- Pull request authors: 2
- Average comments per issue: 0.0
- Average comments per pull request: 0.14
- Merged pull requests: 0
- Bot issues: 0
- Bot pull requests: 5
Top Authors
Issue Authors
- pitmonticone (18)
- ClaudMor (7)
- InterdisciplinaryPhysicsTeam (3)
- Kantishna (1)
- VEZY (1)
- maishaoshao (1)
- bgailleton (1)
- JuliaTagBot (1)
Pull Request Authors
- pitmonticone (56)
- github-actions[bot] (16)
- InterdisciplinaryPhysicsTeam (5)
- TomKellyGenetics (2)
- ClaudMor (1)
- tarleb (1)
- danielskatz (1)
Top Labels
Issue Labels
Pull Request Labels
Packages
- Total packages: 1
- Total downloads: unknown
- Total dependent packages: 0
- Total dependent repositories: 0
- Total versions: 10
juliahub.com: MultilayerGraphs
A Julia package for the creation, manipulation and analysis of the structure, dynamics and functions of multilayer graphs.
- Homepage: https://juliagraphs.org/MultilayerGraphs.jl/dev
- Documentation: https://docs.juliahub.com/General/MultilayerGraphs/stable/
- License: MIT
-
Latest release: 1.1.4
published almost 3 years ago
Rankings
Dependencies
- actions/cache v3 composite
- actions/checkout v3 composite
- codecov/codecov-action v3 composite
- coverallsapp/github-action master composite
- julia-actions/julia-buildpkg v1 composite
- julia-actions/julia-docdeploy v1 composite
- julia-actions/julia-processcoverage v1 composite
- julia-actions/julia-runtest v1 composite
- julia-actions/setup-julia v1.8 composite
- actions/checkout v1 composite
- julia-actions/setup-julia latest composite
- reviewdog/action-suggester v1 composite
- julia-actions/RegisterAction latest composite
- JuliaRegistries/TagBot v1 composite






