MATLABDiffEq
Common interface bindings for the MATLAB ODE solvers via MATLAB.jl for the SciML Scientific Machine Learning ecosystem
Science Score: 54.0%
This score indicates how likely this project is to be science-related based on various indicators:
-
✓CITATION.cff file
Found CITATION.cff file -
✓codemeta.json file
Found codemeta.json file -
✓.zenodo.json file
Found .zenodo.json file -
○DOI references
-
○Academic publication links
-
✓Committers with academic emails
2 of 15 committers (13.3%) from academic institutions -
○Institutional organization owner
-
○JOSS paper metadata
-
○Scientific vocabulary similarity
Low similarity (9.9%) to scientific vocabulary
Keywords
Keywords from Contributors
Repository
Common interface bindings for the MATLAB ODE solvers via MATLAB.jl for the SciML Scientific Machine Learning ecosystem
Basic Info
Statistics
- Stars: 20
- Watchers: 5
- Forks: 12
- Open Issues: 3
- Releases: 10
Topics
Metadata Files
README.md
MATLABDiffEq.jl
MATLABDiffEq.jl is a common interface binding for the MATLAB ordinary differential equation solvers. It uses the MATLAB.jl interop in order to send the differential equation over to MATLAB and solve it. Note that this package requires the differential equation function to be defined using ParameterizedFunctions.jl.
Note that this package isn't for production use and is mostly just for benchmarking and helping new users migrate models over to Julia. For more efficient solvers, see the DifferentialEquations.jl documentation.
Installation
To install MATLABDiffEq.jl, use the following:
julia
using Pkg
Pkg.add("MATLABDiffEq")
Using MATLABDiffEq.jl
MATLABDiffEq.jl is simply a solver on the DiffEq common interface, so for details see the DifferentialEquations.jl documentation.
However, the only options implemented are those for error calculations
(timeseries_error), saveat and tolerances.
Note that the algorithms are defined to have the same name as the MATLAB algorithms,
but are not exported. Thus to use ode45, you would specify the algorithm as
MATLABDiffEq.ode45().
Example
```julia using MATLABDiffEq, ParameterizedFunctions
f = @ode_def LotkaVolterra begin dx = 1.5x - xy dy = -3y + xy end
tspan = (0.0, 10.0) u0 = [1.0, 1.0] prob = ODEProblem(f, u0, tspan) sol = solve(prob, MATLABDiffEq.ode45())
function lorenz(du, u, p, t) du[1] = 10.0(u[2]-u[1]) du[2] = u[1](28.0-u[3]) - u[2] du[3] = u[1]u[2] - (8/3)*u[3] end u0 = [1.0; 0.0; 0.0] tspan = (0.0, 100.0) prob = ODEProblem(lorenz, u0, tspan) sol = solve(prob, MATLABDiffEq.ode45()) ```
Measuring Overhead
To measure the overhead of over the wrapper, note that the variables from the session will be still stored in MATLAB after the computation is done. Thus you can simply call the same ODE function and time it directly. This is done by:
julia
@time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);")
To be even more pedantic, you can play around in the actual MATLAB session by using
MATLABDiffEq.show_msession()
Overhead Amount
Generally, for long enough problems the overhead is minimal. Example:
julia
using DiffEqBase, ParameterizedFunctions, MATLABDiffEq
f = @ode_def_bare RigidBodyBench begin
dy1 = -2*y2*y3
dy2 = 1.25*y1*y3
dy3 = -0.5*y1*y2 + 0.25*sin(t)^2
end
prob = ODEProblem(f, [1.0; 0.0; 0.9], (0.0, 100.0))
alg = MATLABDiffEq.ode45()
algstr = string(typeof(alg).name.name)
For this, we get the following:
```julia julia> @time sol = solve(prob, alg); 0.063918 seconds (38.84 k allocations: 1.556 MB)
julia> @time sol = solve(prob, alg); 0.062600 seconds (38.84 k allocations: 1.556 MB)
julia> @time sol = solve(prob, alg); 0.061438 seconds (38.84 k allocations: 1.556 MB)
julia> @time sol = solve(prob, alg); 0.065460 seconds (38.84 k allocations: 1.556 MB)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);") 0.058249 seconds (11 allocations: 528 bytes)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);") 0.060367 seconds (11 allocations: 528 bytes)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);") 0.060171 seconds (11 allocations: 528 bytes)
julia> @time MATLABDiffEq.eval_string("[t,u] = $(algstr)(diffeqf,tspan,u0,options);") 0.058928 seconds (11 allocations: 528 bytes) ```
Benchmark
The following benchmarks demonstrate a 100x performance advantage for the pure-Julia methods over the MATLAB ODE solvers across a range of stiff and non-stiff ODEs. These were ran with Julia 1.2, MATLAB 2019B, deSolve 1.2.5, and SciPy 1.3.1 after verifying negligible overhead on interop. Note that the MATLAB solvers do outperform that of Python and R.
Non-Stiff Problem 1: Lotka-Volterra
```julia f = @odedefbare LotkaVolterra begin dx = ax - bxy dy = -cy + dxy end a b c d p = [1.5, 1, 3, 1] tspan = (0.0, 10.0) u0 = [1.0, 1.0] prob = ODEProblem(f, u0, tspan, p) sol = solve(prob, Vern7(), abstol = 1/10^14, reltol = 1/10^14) test_sol = TestSolution(sol)
setups = [Dict(:alg=>DP5()) Dict(:alg=>dopri5()) Dict(:alg=>Tsit5()) Dict(:alg=>Vern7()) Dict(:alg=>MATLABDiffEq.ode45()) Dict(:alg=>MATLABDiffEq.ode113()) Dict(:alg=>SciPyDiffEq.RK45()) Dict(:alg=>SciPyDiffEq.LSODA()) Dict(:alg=>SciPyDiffEq.odeint()) Dict(:alg=>deSolveDiffEq.lsoda()) Dict(:alg=>deSolveDiffEq.ode45()) Dict(:alg=>CVODE_Adams())]
names = ["Julia: DP5" "Hairer: dopri5" "Julia: Tsit5" "Julia: Vern7" "MATLAB: ode45" "MATLAB: ode113" "SciPy: RK45" "SciPy: LSODA" "SciPy: odeint" "deSolve: lsoda" "deSolve: ode45" "Sundials: Adams"]
abstols = 1.0 ./ 10.0 .^ (6:13) reltols = 1.0 ./ 10.0 .^ (3:10) wp = WorkPrecisionSet(prob, abstols, reltols, setups; names = names, appxsol = testsol, dense = false, saveeverystep = false, numruns = 100, maxiters = 10000000, timeseries_errors = false, verbose = false) plot(wp, title = "Non-stiff 1: Lotka-Volterra") ```

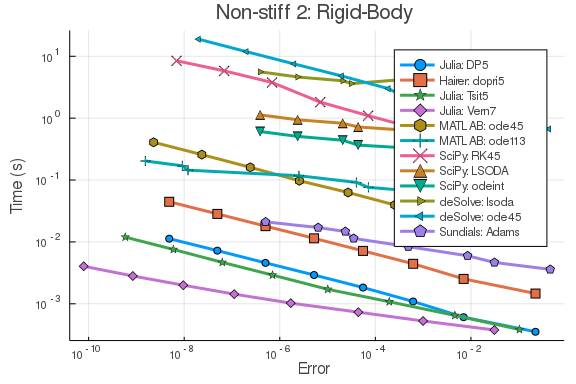
Non-Stiff Problem 2: Rigid Body
```julia f = @odedefbare RigidBodyBench begin dy1 = -2y2y3 dy2 = 1.25y1y3 dy3 = -0.5y1y2 + 0.25*sin(t)^2 end prob = ODEProblem(f, [1.0; 0.0; 0.9], (0.0, 100.0)) sol = solve(prob, Vern7(), abstol = 1/10^14, reltol = 1/10^14) test_sol = TestSolution(sol)
setups = [Dict(:alg=>DP5()) Dict(:alg=>dopri5()) Dict(:alg=>Tsit5()) Dict(:alg=>Vern7()) Dict(:alg=>MATLABDiffEq.ode45()) Dict(:alg=>MATLABDiffEq.ode113()) Dict(:alg=>SciPyDiffEq.RK45()) Dict(:alg=>SciPyDiffEq.LSODA()) Dict(:alg=>SciPyDiffEq.odeint()) Dict(:alg=>deSolveDiffEq.lsoda()) Dict(:alg=>deSolveDiffEq.ode45()) Dict(:alg=>CVODE_Adams())]
names = ["Julia: DP5" "Hairer: dopri5" "Julia: Tsit5" "Julia: Vern7" "MATLAB: ode45" "MATLAB: ode113" "SciPy: RK45" "SciPy: LSODA" "SciPy: odeint" "deSolve: lsoda" "deSolve: ode45" "Sundials: Adams"]
abstols = 1.0 ./ 10.0 .^ (6:13) reltols = 1.0 ./ 10.0 .^ (3:10) wp = WorkPrecisionSet(prob, abstols, reltols, setups; names = names, appxsol = testsol, dense = false, saveeverystep = false, numruns = 100, maxiters = 10000000, timeseries_errors = false, verbose = false) plot(wp, title = "Non-stiff 2: Rigid-Body") ```
Stiff Problem 1: ROBER
```julia rober = @odedef begin dy₁ = -k₁y₁+k₃y₂y₃ dy₂ = k₁y₁-k₂y₂^2-k₃y₂y₃ dy₃ = k₂y₂^2 end k₁ k₂ k₃ prob = ODEProblem(rober, [1.0, 0.0, 0.0], (0.0, 1e5), [0.04, 3e7, 1e4]) sol = solve(prob, CVODEBDF(), abstol = 1/10^14, reltol = 1/10^14) test_sol = TestSolution(sol)
abstols = 1.0 ./ 10.0 .^ (7:8) reltols = 1.0 ./ 10.0 .^ (3:4);
setups = [Dict(:alg=>Rosenbrock23()) Dict(:alg=>TRBDF2()) Dict(:alg=>RadauIIA5()) Dict(:alg=>rodas()) Dict(:alg=>radau()) Dict(:alg=>MATLABDiffEq.ode23s()) Dict(:alg=>MATLABDiffEq.ode15s()) Dict(:alg=>SciPyDiffEq.LSODA()) Dict(:alg=>SciPyDiffEq.BDF()) Dict(:alg=>SciPyDiffEq.odeint()) Dict(:alg=>deSolveDiffEq.lsoda()) Dict(:alg=>CVODE_BDF())]
names = ["Julia: Rosenbrock23" "Julia: TRBDF2" "Julia: radau" "Hairer: rodas" "Hairer: radau" "MATLAB: ode23s" "MATLAB: ode15s" "SciPy: LSODA" "SciPy: BDF" "SciPy: odeint" "deSolve: lsoda" "Sundials: CVODE"]
wp = WorkPrecisionSet(prob, abstols, reltols, setups; names = names, printnames = true, dense = false, verbose = false, saveeverystep = false, appxsol = test_sol, maxiters = Int(1e5)) plot(wp, title = "Stiff 1: ROBER", legend = :topleft) ```

Stiff Problem 2: HIRES
```julia f = @ode_def Hires begin dy1 = -1.71y1 + 0.43y2 + 8.32y3 + 0.0007 dy2 = 1.71y1 - 8.75y2 dy3 = -10.03y3 + 0.43y4 + 0.035y5 dy4 = 8.32y2 + 1.71y3 - 1.12y4 dy5 = -1.745y5 + 0.43y6 + 0.43y7 dy6 = -280.0y6y8 + 0.69y4 + 1.71y5 - 0.43y6 + 0.69y7 dy7 = 280.0y6y8 - 1.81y7 dy8 = -280.0y6y8 + 1.81y7 end
u0 = zeros(8) u0[1] = 1 u0[8] = 0.0057 prob = ODEProblem(f, u0, (0.0, 321.8122))
sol = solve(prob, Rodas5(), abstol = 1/10^14, reltol = 1/10^14) test_sol = TestSolution(sol)
abstols = 1.0 ./ 10.0 .^ (5:8) reltols = 1.0 ./ 10.0 .^ (1:4);
setups = [Dict(:alg=>Rosenbrock23()) Dict(:alg=>TRBDF2()) Dict(:alg=>RadauIIA5()) Dict(:alg=>rodas()) Dict(:alg=>radau()) Dict(:alg=>MATLABDiffEq.ode23s()) Dict(:alg=>MATLABDiffEq.ode15s()) Dict(:alg=>SciPyDiffEq.LSODA()) Dict(:alg=>SciPyDiffEq.BDF()) Dict(:alg=>SciPyDiffEq.odeint()) Dict(:alg=>deSolveDiffEq.lsoda()) Dict(:alg=>CVODE_BDF())]
names = ["Julia: Rosenbrock23" "Julia: TRBDF2" "Julia: radau" "Hairer: rodas" "Hairer: radau" "MATLAB: ode23s" "MATLAB: ode15s" "SciPy: LSODA" "SciPy: BDF" "SciPy: odeint" "deSolve: lsoda" "Sundials: CVODE"]
wp = WorkPrecisionSet(prob, abstols, reltols, setups; names = names, printnames = true, saveeverystep = false, appxsol = test_sol, maxiters = Int(1e5), numruns = 100) plot(wp, title = "Stiff 2: Hires", legend = :topleft) ```

Owner
- Name: SciML Open Source Scientific Machine Learning
- Login: SciML
- Kind: organization
- Email: contact@chrisrackauckas.com
- Website: https://sciml.ai
- Twitter: SciML_Org
- Repositories: 170
- Profile: https://github.com/SciML
Open source software for scientific machine learning
Citation (CITATION.bib)
@article{DifferentialEquations.jl-2017,
author = {Rackauckas, Christopher and Nie, Qing},
doi = {10.5334/jors.151},
journal = {The Journal of Open Research Software},
keywords = {Applied Mathematics},
note = {Exported from https://app.dimensions.ai on 2019/05/05},
number = {1},
pages = {},
title = {DifferentialEquations.jl – A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia},
url = {https://app.dimensions.ai/details/publication/pub.1085583166 and http://openresearchsoftware.metajnl.com/articles/10.5334/jors.151/galley/245/download/},
volume = {5},
year = {2017}
}
GitHub Events
Total
- Delete event: 4
- Push event: 2
- Pull request event: 7
- Create event: 3
Last Year
- Delete event: 4
- Push event: 2
- Pull request event: 7
- Create event: 3
Committers
Last synced: 8 months ago
Top Committers
| Name | Commits | |
|---|---|---|
| Christopher Rackauckas | a****s@c****m | 53 |
| ChrisRackauckas | c****s@g****m | 14 |
| Christopher Rackauckas | C****t@C****m | 13 |
| github-actions[bot] | 4****] | 9 |
| Utkarsh | r****0@g****m | 7 |
| Anant Thazhemadam | a****m@g****m | 1 |
| Anshul Singhvi | a****7@s****u | 1 |
| Chris de Graaf | me@c****v | 1 |
| Hendrik Ranocha | m****l@r****e | 1 |
| Pepijn de Vos | p****s@j****m | 1 |
| ScottPJones | s****s@a****u | 1 |
| Yingbo Ma | m****5@g****m | 1 |
| David Widmann | d****n | 1 |
| Julia TagBot | 5****t | 1 |
| dependabot[bot] | 4****] | 1 |
Committer Domains (Top 20 + Academic)
Issues and Pull Requests
Last synced: 6 months ago
All Time
- Total issues: 11
- Total pull requests: 28
- Average time to close issues: about 2 months
- Average time to close pull requests: 3 days
- Total issue authors: 8
- Total pull request authors: 13
- Average comments per issue: 4.91
- Average comments per pull request: 0.21
- Merged pull requests: 25
- Bot issues: 0
- Bot pull requests: 11
Past Year
- Issues: 0
- Pull requests: 0
- Average time to close issues: N/A
- Average time to close pull requests: N/A
- Issue authors: 0
- Pull request authors: 0
- Average comments per issue: 0
- Average comments per pull request: 0
- Merged pull requests: 0
- Bot issues: 0
- Bot pull requests: 0
Top Authors
Issue Authors
- rohith14 (3)
- ChrisRackauckas (2)
- utkarsh530 (1)
- AshtonSBradley (1)
- PallHaraldsson (1)
- ArnoStrouwen (1)
- JuliaTagBot (1)
- NirvikNU (1)
Pull Request Authors
- github-actions[bot] (10)
- ChrisRackauckas (7)
- dependabot[bot] (3)
- utkarsh530 (3)
- thazhemadam (2)
- christopher-dG (2)
- ScottPJones (1)
- ranocha (1)
- YingboMa (1)
- devmotion (1)
- asinghvi17 (1)
- pepijndevos (1)
- JuliaTagBot (1)
Top Labels
Issue Labels
Pull Request Labels
Packages
- Total packages: 1
-
Total downloads:
- julia 1 total
- Total dependent packages: 0
- Total dependent repositories: 0
- Total versions: 10
juliahub.com: MATLABDiffEq
Common interface bindings for the MATLAB ODE solvers via MATLAB.jl for the SciML Scientific Machine Learning ecosystem
- Documentation: https://docs.juliahub.com/General/MATLABDiffEq/stable/
- License: MIT
-
Latest release: 1.2.0
published almost 3 years ago