M²E³D: Multiphase Materials Exploration via Evolutionary Equation Discovery

Driving simulational & experimental discovery, from the micro to the macro

M²E³D discovers equations, models and correlations underpinning experimental data.

It builds on the fantastic PySR and fvGP libraries to build a user-facing package offering:

• Discovery of symbolic closed-form equations that model multiple responses.
• Efficient parameter sampling for planning experimental / simulational campaigns.
• System multi-response uncertainty quantification - and specifically targeting high-variance parameter regions.
• Automatic parallelisation of complex user simulation scripts on OS Processes and distributed supercomputers.
• Interactive plotting of responses, uncertainties, discovered model outputs.
• Language-agnostic saving of results found.

M²E³D was developed to discover physical laws and correlations in chemical engineering, but it is data-agnostic - and works with both simulated and experimental results in any domain.

System Response Exploration

How does a system behave under different conditions? E.g. drag force acting on a sphere for different flow velocities. M²E³D can explore multiple responses in one of two ways:

1. Locally / manually: running experiments / simulations, then feeding results back to MED.
2. Massively parallel: for complex simulations that can be launched in Python, MED can automatically change simulation parameters and run them in parallel on OS processes (locally) or SLURM jobs (distributed clusters).

Show me some Code!

Here is a minimal example showing the main interface to the medeq.MED object. For automatic parallelisation and other features, see the docs.

```python import medeq import numpy as np

Create DataFrame of MED free parameters and their bounds

parameters = medeq.create_parameters( ["velocity", "viscosity", "radius"], minimums = [-9, -9, -9], maximums = [10, 10, 10], )

def instrument(x): '''Example unknown "experimental response" - a complex non-convex function. ''' return x[0] * np.sin(0.5 * x[1]) + np.cos(1.1 * x[2])

Create MED object, keeping track of free parameters, samples and results

med = medeq.MED(parameters)

Initial parameter sampling

med.sample(24) med.evaluate(instrument)

New sampling, targeting most uncertain parameter regions

med.sample(16) med.evaluate(instrument)

Add previous / manually-evaluated responses

med.augment([[0, 0, 0]], [1])

Save all results to disk - you can load them on another machine

med.save("med_results")

Discover underlying equation; tell MED what operators it may use

med.discover( binaryoperators = ["+", "-", "*", "/"], unaryoperators = ["cos"], )

Plot interactive 2D slices of responses and uncertainties

med.plot_gp() ```

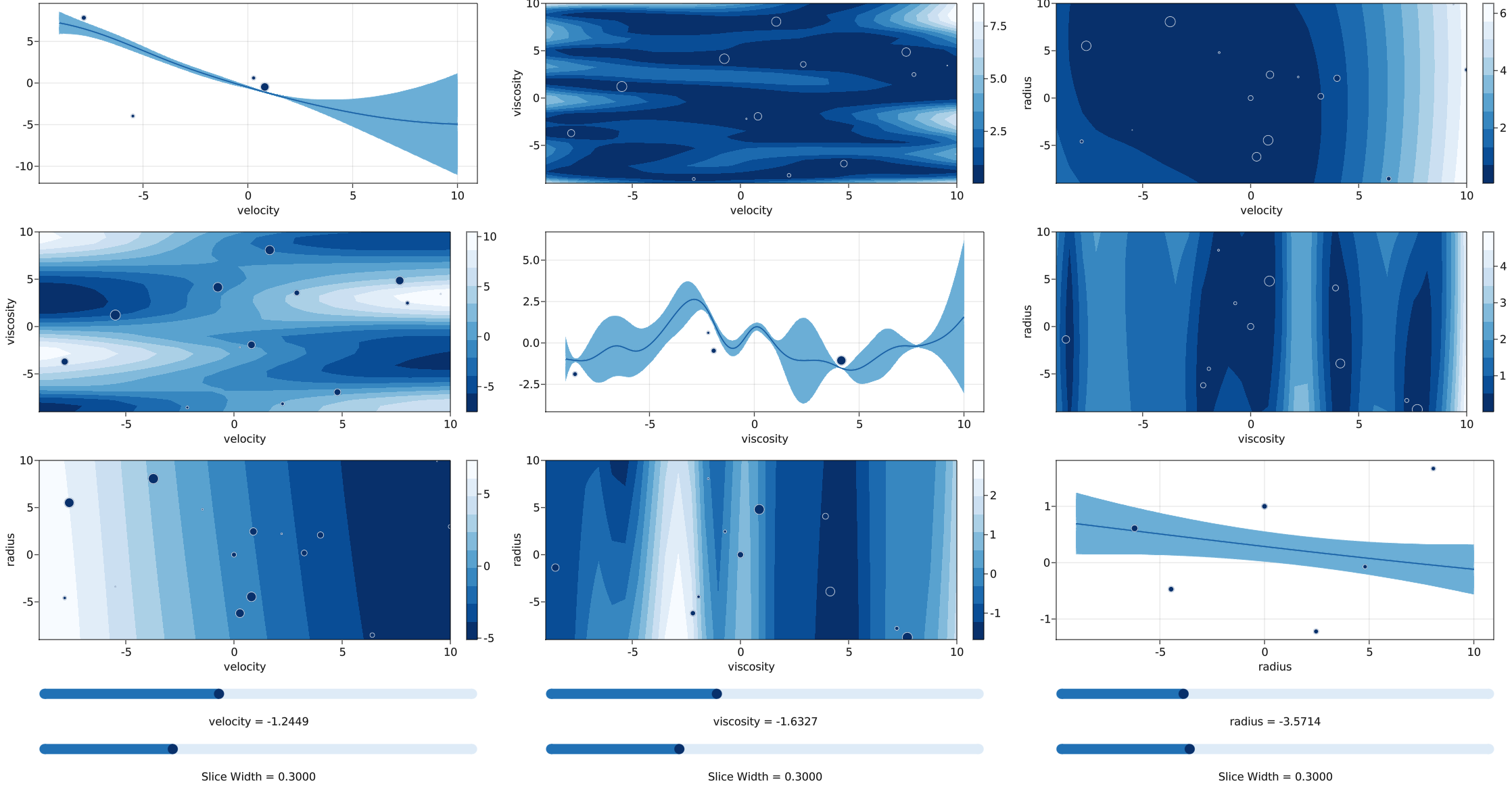
Here are the equations found by SymbolicRegression.jl at various complexity levels:

```

Hall of Fame:

Complexity Loss Score Equation 1 1.656e+01 1.025e-07 -0.19632196 2 1.626e+01 1.812e-02 cos(radius) 3 1.541e+01 5.332e-02 (-0.20152433 * velocity) 4 1.227e+01 2.278e-01 (velocity * cos(velocity)) 6 8.668e+00 1.739e-01 (velocity * cos(-1.0899653 * velocity)) 8 4.988e-01 1.428e+00 (velocity * cos(1.5935777 + (-0.50125474 * viscosity))) 10 4.946e-01 4.271e-03 ((-1.016915 * velocity) * cos(7.8330894 + (0.5005289 * viscosity))) 11 1.241e-01 1.383e+00 (cos(radius) + (velocity * cos(1.5515859 + (-0.49880704 * viscosity)))) 13 0.000e+00 1.151e+01 (cos(1.1000026 * radius) + (velocity * cos(1.5707898 + (-0.50000036 * viscosity)))) ```

Note how it discovered the sin(x) term as cos(1.57 + x).

Getting Started

Before the medeq library is published to PyPI, you can install it directly from this GitHub repository:

$> pip install git+https://github.com/uob-positron-imaging-centre/MED

Alternatively, you can download all the code and run pip install . inside its directory:

$> git clone https://github.com/uob-positron-imaging-centre/MED $> cd MED $MED> pip install .

If you would like to modify the source code and see your changes without reinstalling the package, use the -e flag for a development installation:

$MED> pip install -e .

Julia

To discover underlying equations and see interactive plots of system responses, uncertainties and model outputs, you need to install Julia (a beautiful, high-performance programming language) on your system and the PySR library:

1. Install Julia manually (see Julia downloads, version >=1.8 is recommended).
2. import medeq; medeq.install()

Autonomously Explore System Responses...

... and discover underlying physical laws / correlations.

Exploring systems responses can be done in one of two ways:

1. Locally / manually: running experiments / simulations, then feeding results back to MED.
2. Massively parallel: for complex simulations that can be launched in Python, MED can automatically change simulation parameters and run them in parallel on OS processes (locally) or SLURM jobs (distributed clusters).

A typical local workflow is:

1. Define free parameters to explore as a pd.DataFrame - you can use the medeq.create_parameters function for this.

```python

import medeq parameters = medeq.create_parameters( ["A", "B"], minimums = [-5., -5.], maximums = [10., 10.], ) print(parameters) value min max A 2.5 -5.0 10.0 B 2.5 -5.0 10.0 ```

1. Create a medeq.MED object and generate samples (i.e. parameter combinations) to evaluate - the default sampler covers the parameter space as efficiently as possible, taking previous results into account; use the MED.sample(n) method to get n samples to try.

```python

med = medeq.MED(parameters, seed = 42) print(med)

MED(seed=42)

parameters = value min max A 2.5 -5.0 10.0 B 2.5 -5.0 10.0 response_names =

None

sampler = DVASampler(d=2, seed=42) samples = np.ndarray[(0, 2), float64] responses = NoneType epochs = list[0, tuple[int, int]]

med.sample(5) array([[-3.33602115, -0.45639296], [ 5.55496225, 5.554965 ], [ 2.72771903, -3.48852585], [-0.45639308, 8.33602069], [ 8.48852568, 2.27228172]]) ```

1. For a local / offline workflow, these samples can be evaluated in one of two ways:

• Evaluate samples manually, offline - i.e. run experiments, simulations, etc. and feed them back to MED.
• Let MED evaluate a simple Python function / model.

```python

Evaluate samples manually - run experiments, simulations, etc.

to_evaluate = med.queue responses = [1, 2, 3, 4, 5] med.evaluate(responses)

Or evaluate simple Python function / model

def instrument(sample): return sample[0] + sample[1]

med.evaluate(instrument) med.results A B variance response 0 -3.336021 -0.456393 0.037924 -3.792414 1 5.554962 5.554965 0.111099 11.109927 2 2.727719 -3.488526 0.007608 -0.760807 3 -0.456393 8.336021 0.078796 7.879628 4 8.488526 2.272282 0.107608 10.760807 ```

For a massively parallel workflow, e.g. using a complex simulation, all you need is a standalone Python script that:

• Defines its free parameters between two # MED PARAMETERS START / END directives.
• Runs the simulation in any way - define simulation inline, launch it on a supercomputer and collect results, etc.
• Defines a variable "response" for the simulated output of interest - either as a single number or a list of numbers (multi-response), or a dictionary with names for each response.

Here is a simple example of a MED script:

```python

In file simulation_script.py

MED PARAMETERS START

import medeq

parameters = medeq.create_parameters( ["A", "B", "C"], [-5., -5., -5.], [10., 10., 10.], )

MED PARAMETERS END

Run simulation in any way, locally, on a supercomputer and collect

results - then define the variable response (float or list[float])

values = parameters["value"] response = values["A"]2 + values["B"]2 ```

If you have previous, separate experimental data, you can MED.augment the dataset of responses:

```python

Augment dataset of responses with historical data

samples = [ [1, 1], [2, 2], [1, 2], ]

responses = [1, 2, 3] med.augment(samples, responses) ```

And now discover underlying equations!

```python

med.discover(binary_operators = ["+", "*"])

Hall of Fame:

Complexity Loss Score Equation 1 2.412e+01 5.296e-01 B 3 0.000e+00 1.151e+01 (A + B) ```

Contributing

You are more than welcome to contribute to this package in the form of library improvements, documentation or helpful examples; please submit them either as:

• GitHub issues.
• Pull requests.
• Email me at a.l.nicusan@bham.ac.uk.

Acknowledgements & Funding

The authors gratefully acknowledge the following funding, without which M²E³D would not have been possible:

M²E³D: Multiphase Materials Exploration via Evolutionary Equation Discovery
Royce Materials 4.0 Feasibility and Pilot Scheme Grant, £57,477

Citing

If you use this library in your research, you are kindly asked to cite:

Nicusan, A., & Windows-Yule, K. (2022). M2E3D: Multiphase Materials Exploration via Evolutionary Equation Discovery (Version 0.1.0) [Computer software]

This library would not have been possible without the excellent PySR and fvGP packages, which form the very core of the symbolic regression and Gaussian Process engines. If you use medeq in your published work, please also cite:

Miles Cranmer. (2020). MilesCranmer/PySR v0.2 (v0.2). Zenodo. https://doi.org/10.5281/zenodo.4041459

Marcus Michael Noack, Ian Humphrey, elliottperryman, Ronald Pandolfi, & MarcusMichaelNoack. (2022). lbl-camera/fvGP: (3.2.11). Zenodo. https://doi.org/10.5281/zenodo.6147361

Licensing

The medeq library is published under the GPL v3.0 license.