Data

Tools

Indexes

Applications

Experiments

Open Source Science

BifurcationKit

A Julia package to perform Bifurcation Analysis

https://github.com/bifurcationkit/bifurcationkit.jl

Science Score: 44.0%

This score indicates how likely this project is to be science-related based on various indicators:

  • ✓
    CITATION.cff file
    Found CITATION.cff file
  • ✓
    codemeta.json file
    Found codemeta.json file
  • ✓
    .zenodo.json file
    Found .zenodo.json file
  • ○
    DOI references
  • ○
    Academic publication links
  • ○
    Academic email domains
  • ○
    Institutional organization owner
  • ○
    JOSS paper metadata
  • ○
    Scientific vocabulary similarity
    Low similarity (13.5%) to scientific vocabulary

Keywords

bifurcation bifurcation-diagram codim2 continuation deflation floquet gpu hopf-point newton-krylov pde periodic-orbits pseudo-arclength-continuation
Last synced: 6 months ago · JSON representation ·

Repository

A Julia package to perform Bifurcation Analysis

Basic Info
Statistics
  • Stars: 333
  • Watchers: 10
  • Forks: 42
  • Open Issues: 28
  • Releases: 48
Topics
bifurcation bifurcation-diagram codim2 continuation deflation floquet gpu hopf-point newton-krylov pde periodic-orbits pseudo-arclength-continuation
Created about 7 years ago · Last pushed 6 months ago
Metadata Files
Readme Changelog License Citation Authors

README.md

BifurcationKit.jl

| Documentation | Build Status | Coverage | Version / Stats | | :-: | :-: | :-: | :-: | | | Build status | codecov | ver-img | | | Build status | | deps-img downloads|

This Julia package aims at performing automatic bifurcation analysis of possibly large dimensional equations F(u, λ)=0 where λ is real by taking advantage of iterative methods, dense / sparse formulation and specific hardwares (e.g. GPU).

It incorporates continuation algorithms (PALC, deflated continuation, ...) based on a Newton-Krylov method to correct the predictor step and a Matrix-Free/Dense/Sparse eigensolver is used to compute stability and bifurcation points.

The idea is to be able to seamlessly switch the continuation algorithm a bit like changing the time stepper (Euler, RK4,...) for ODEs.

BifurcationKit can also seek for periodic orbits of Cauchy problems. It is by now, one of the only software which provides shooting methods and methods based on finite differences / collocation to compute periodic orbits.

The current focus is on large scale nonlinear problems and multiple hardwares. Hence, the goal is to provide Matrix Free methods on GPU (see PDE example and Periodic orbit example) or on cluster to study non linear PDE, nonlocal problems, compute sub-manifolds...

Despite this focus, the package can easily handle low dimensional problems and specific optimizations are regularly added.

SciML Integration

BifurcationKit.jl is listed in Third patry parameter analysis of SciML Docs under the "Analysis" menu. ModelingToolkit.jl and Catalyst.jl rely on BifurcationKit.jl as external dependency.

📚 Support and citation

If you use BifurcationKit.jl in your work, we ask that you cite the following paper on HAL-Inria with bibtex entry CITATION.bib. Open source development as part of academic research strongly depends on this. Please also consider starring this repository if you like our work, this will help us to secure funding in the future.

📦 Installation

This package requires Julia >= v1.3.0

To install it, please run

] add BifurcationKit

To install the bleeding edge version, please run

] add BifurcationKit#master

🧩 Plugins

Most plugins are located in the organization bifurcationkit:

Overview of capabilities

The list of capabilities is available here.

Examples of bifurcation diagrams (ODEs and PDEs)

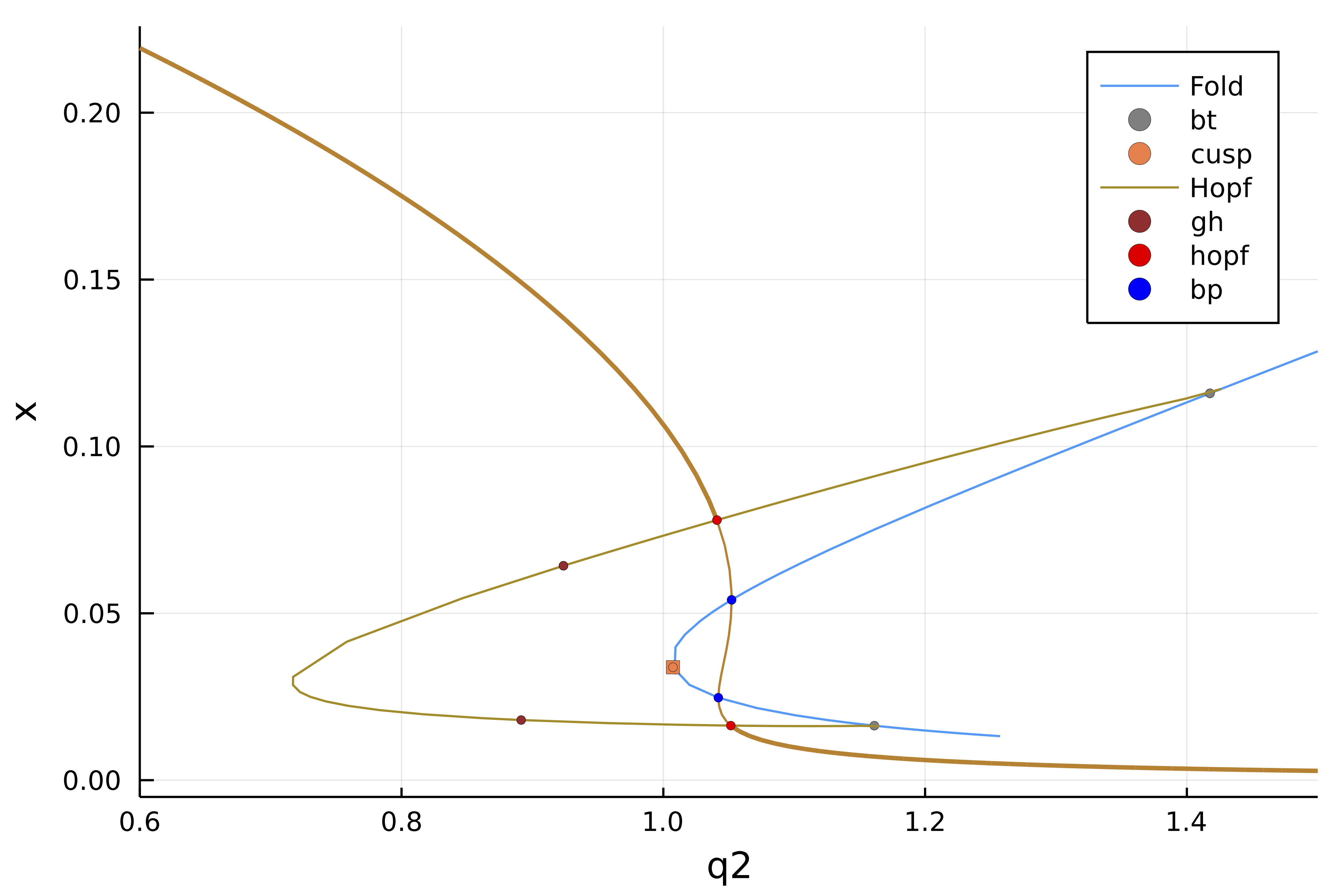
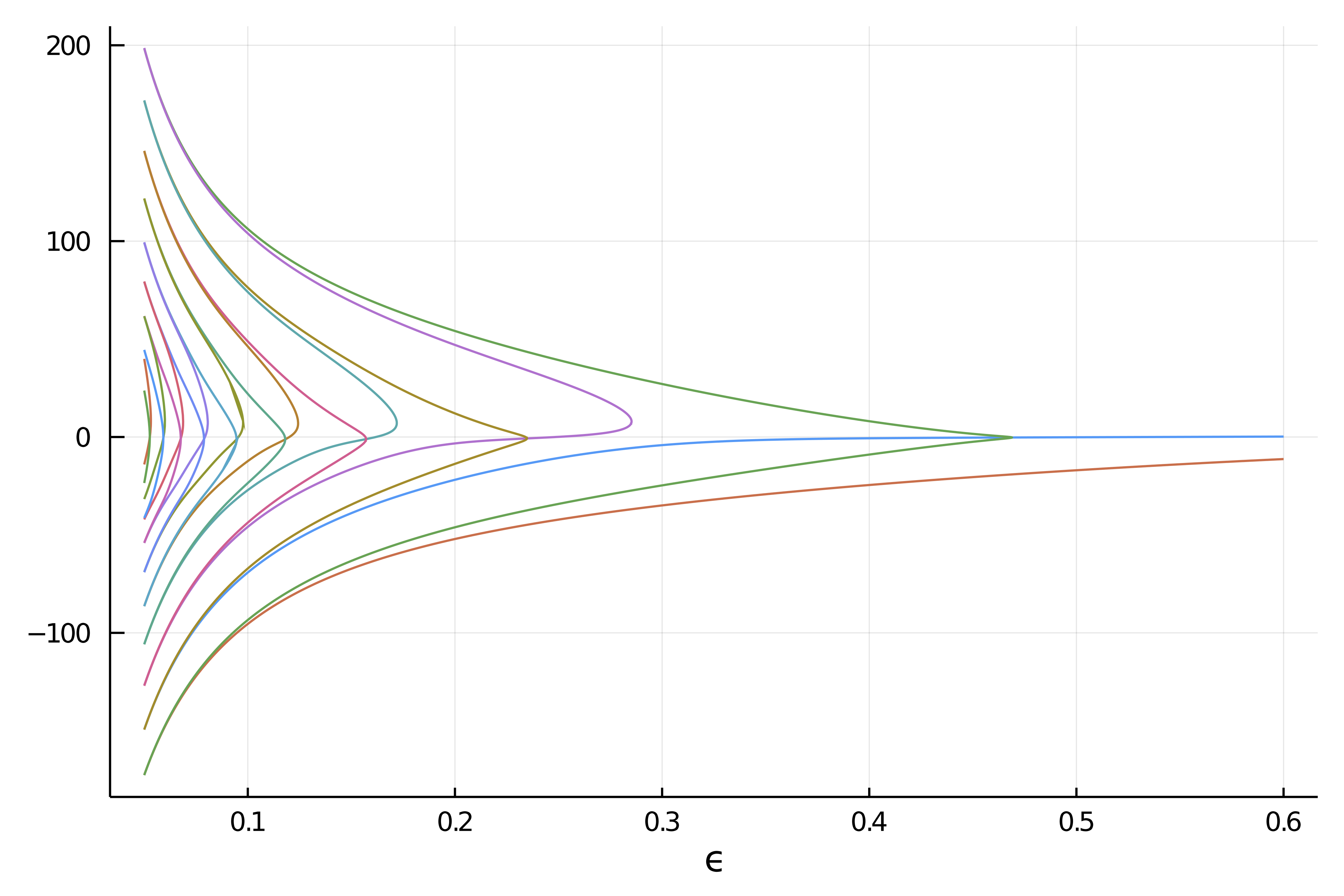
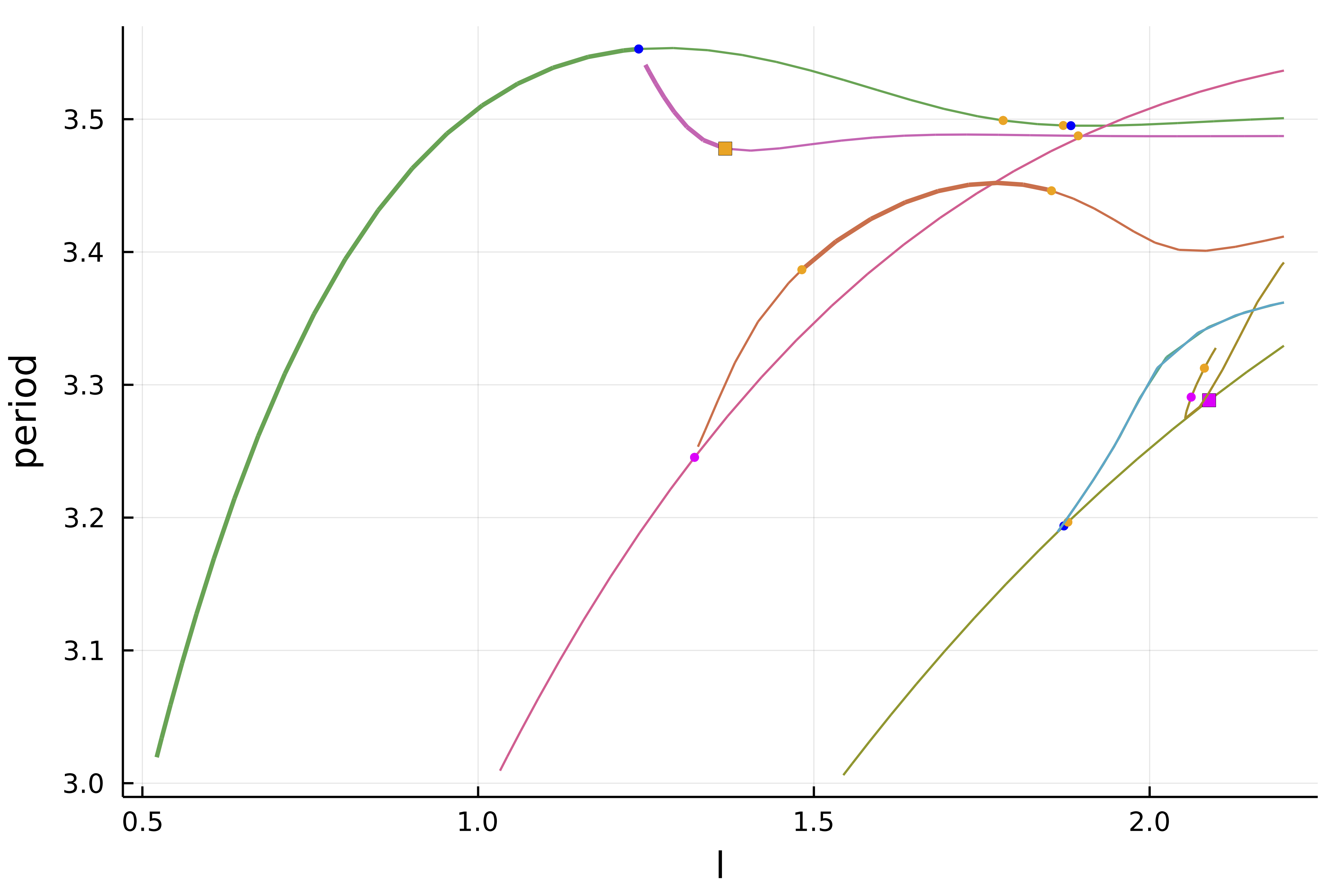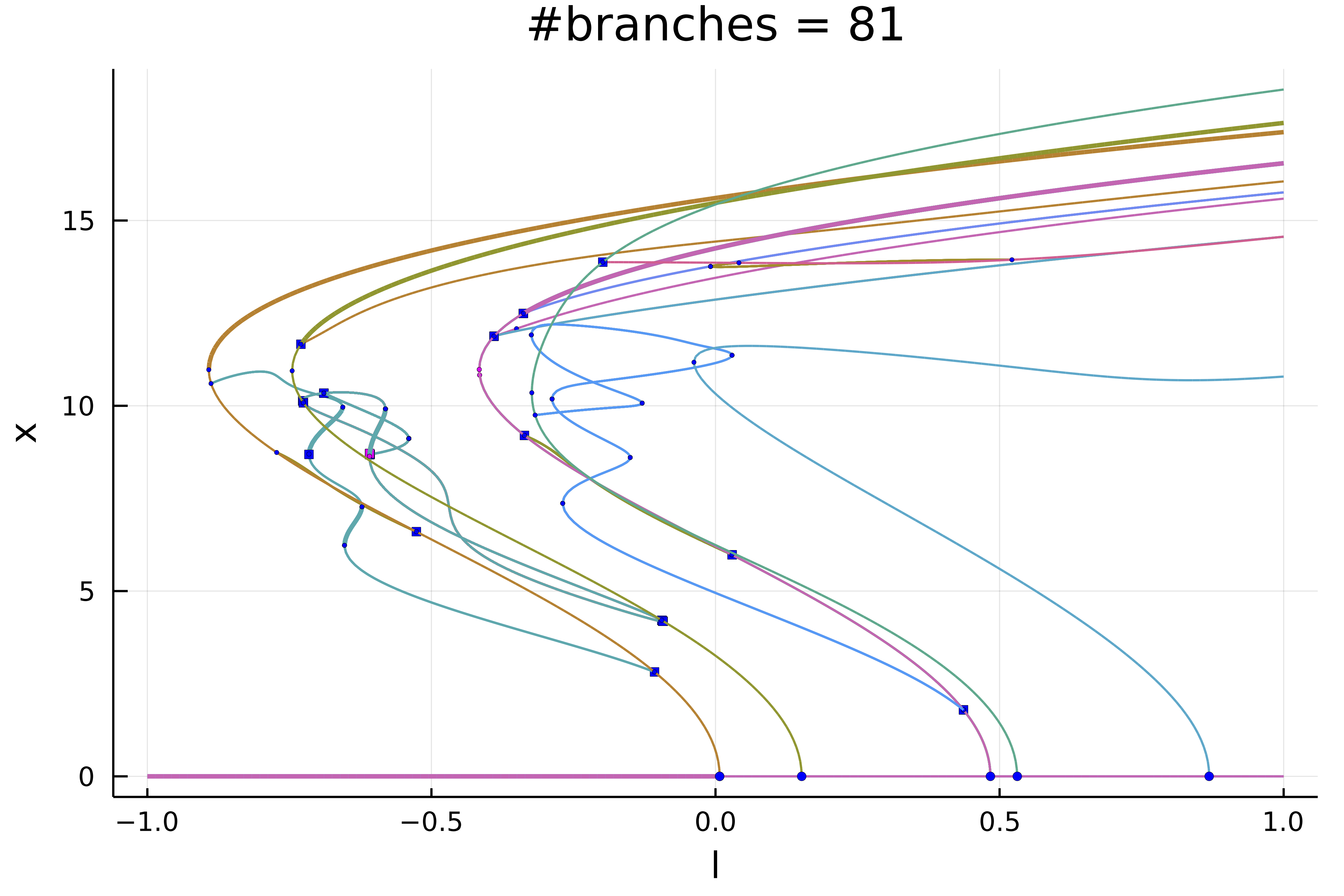
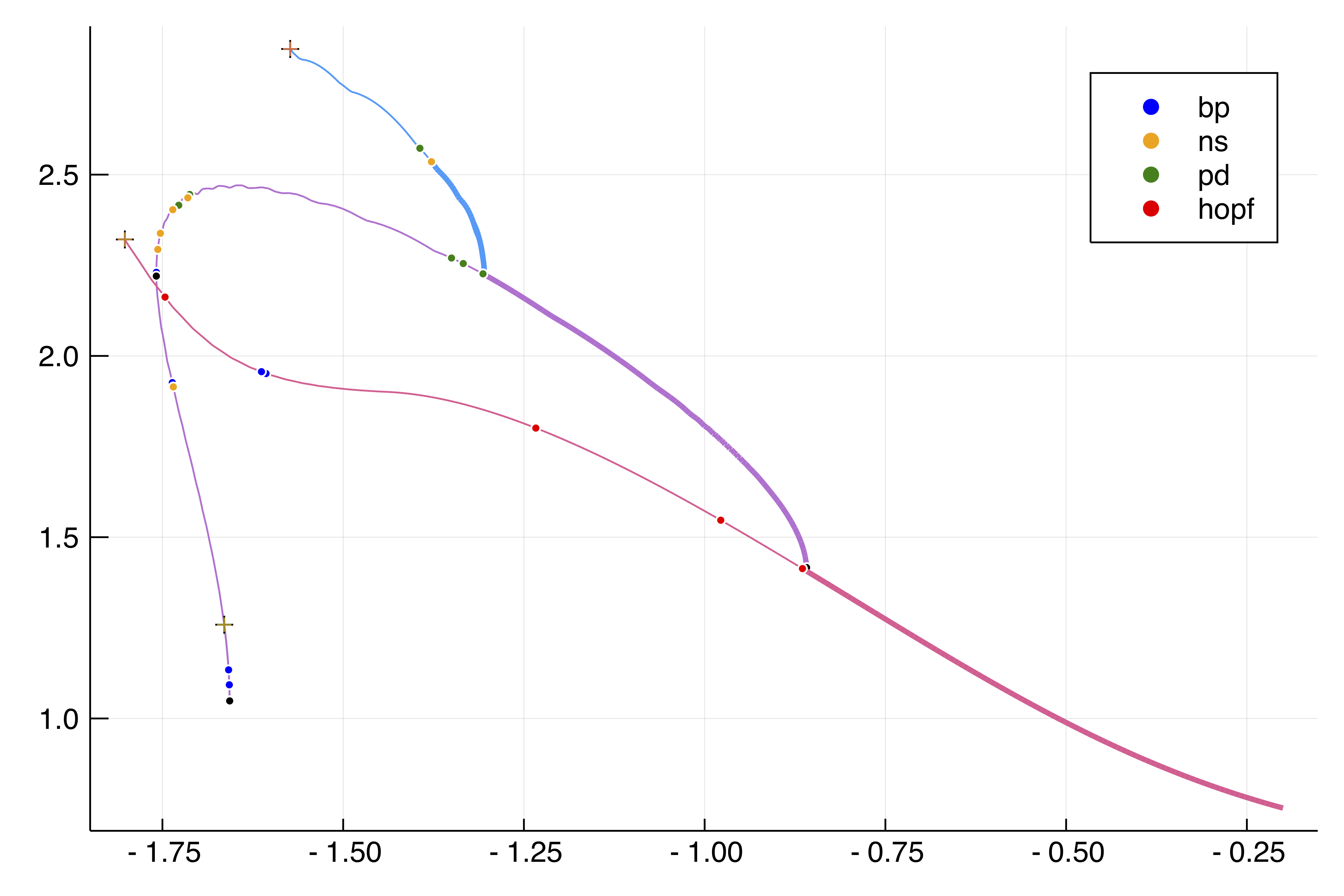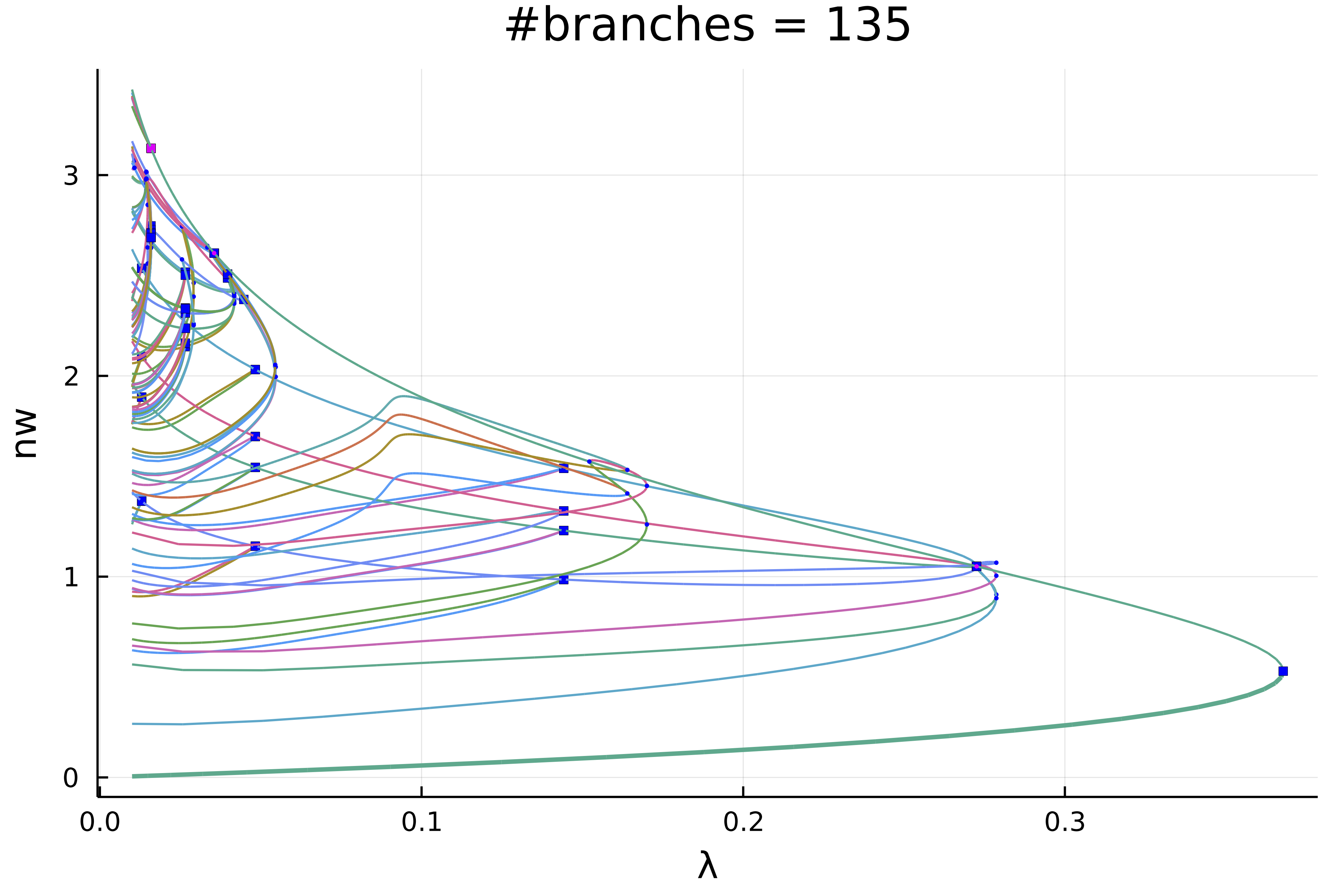
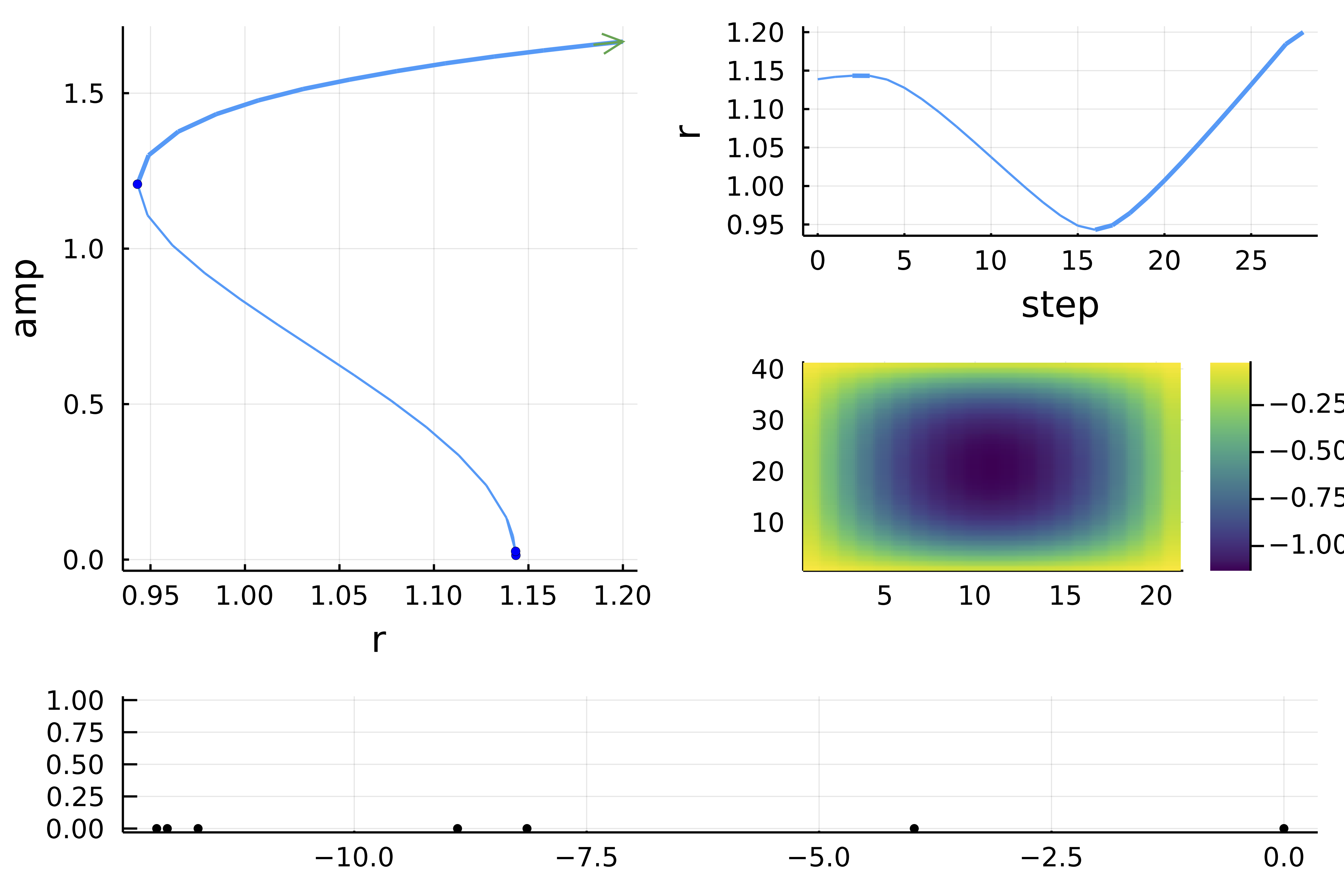
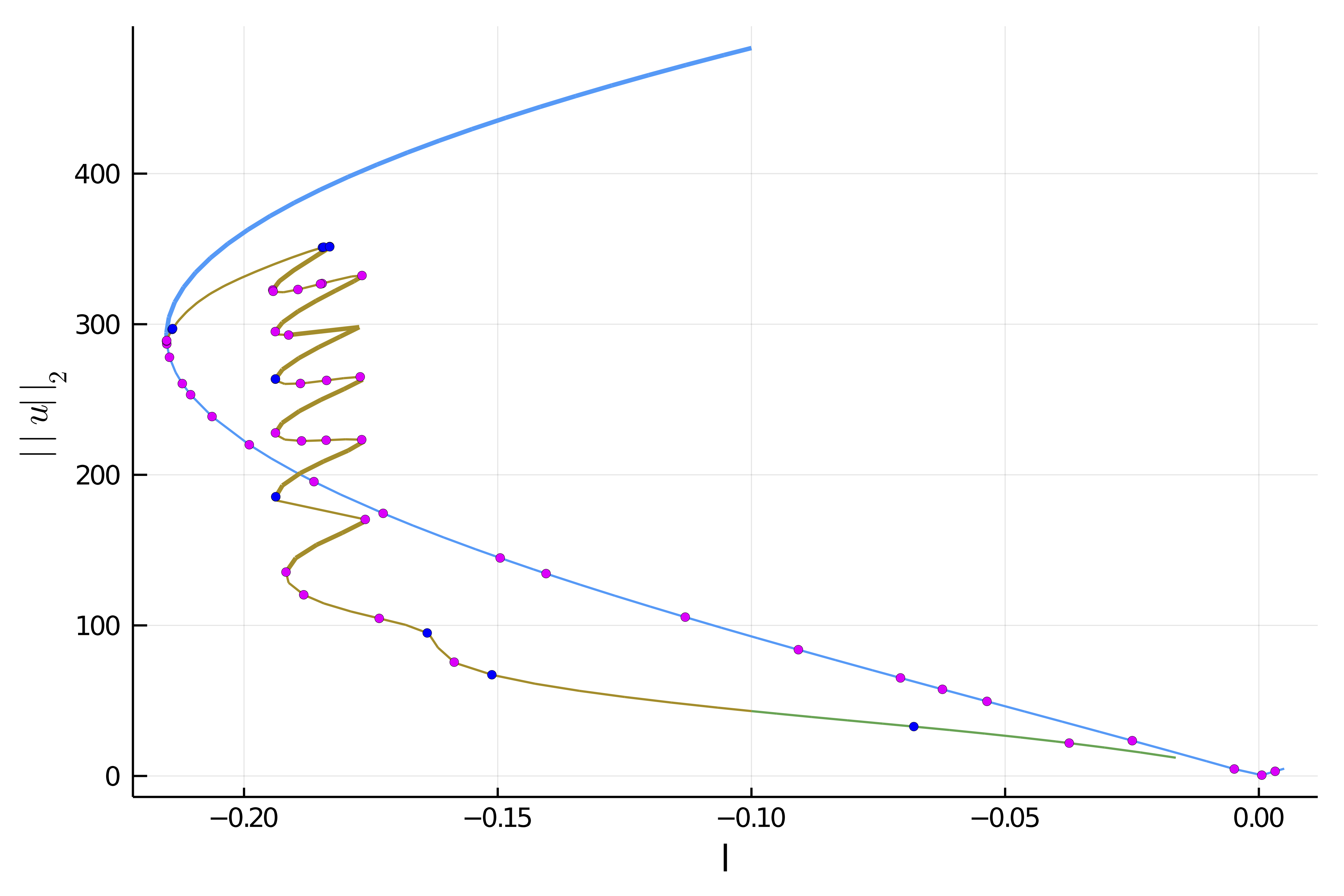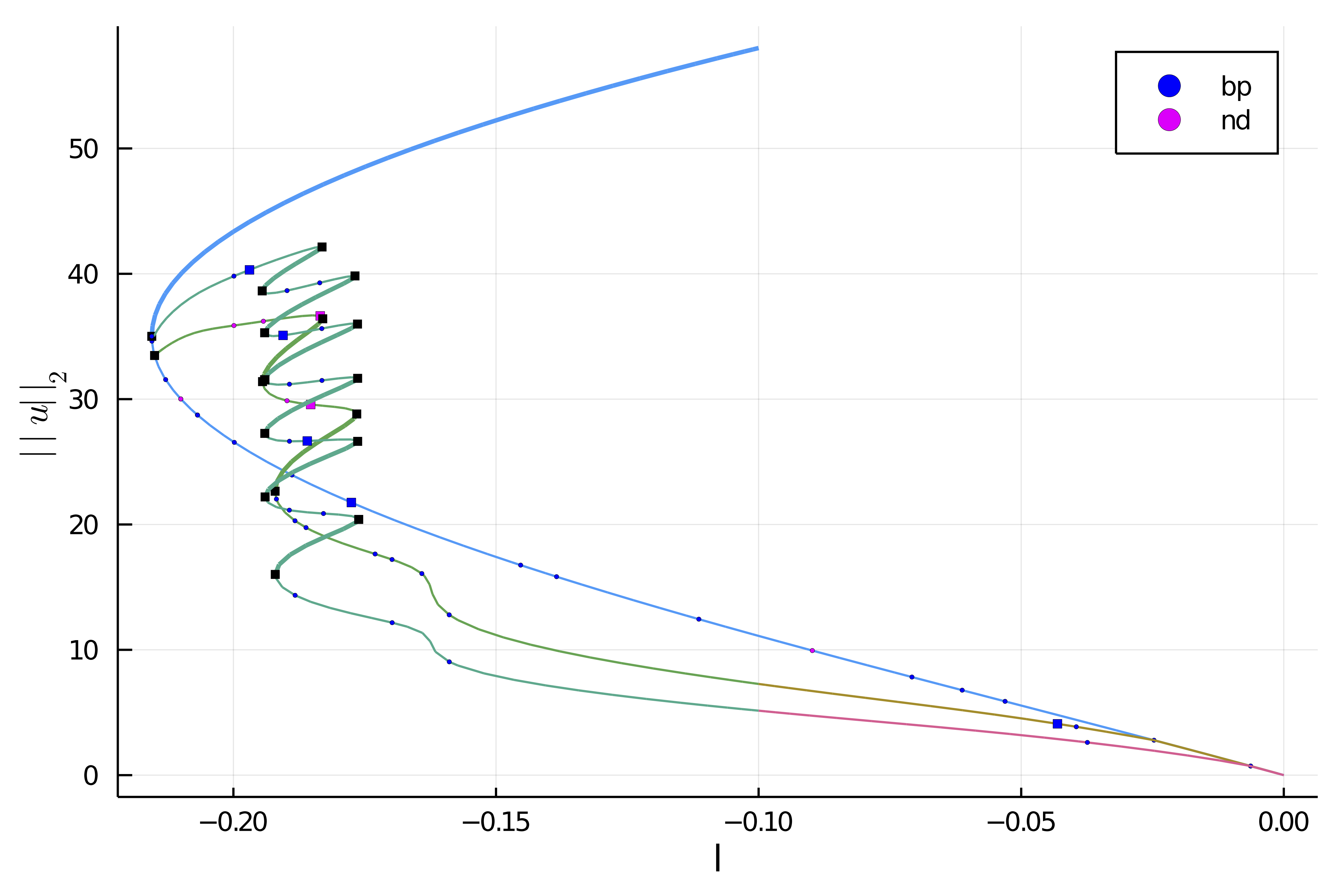
| | | |:-------------:|:-------------:| | simple ODE example | Codimension 2 (ODE) | | | | | Automatic Bif. Diagram in 1D Swift Hohenberg | Automatic Bif. Diagram in 2D Bratu | | | | | Snaking in 2D Swift Hohenberg | Periodic orbits in 1D Brusselator | | | | Period doubling BVAM Model | Periodic orbits in 2D Ginzburg-Landau | | | | | Deflated Continuation in Carrier problem | 2D Swift Hohenberg on GPU |

Owner

  • Name: BifurcationKit
  • Login: bifurcationkit
  • Kind: organization

Open source software for automatic numerical bifurcation analysis

Citation (CITATION.bib) 

@misc{veltz:hal-02902346,
  title = {{BifurcationKit.jl}},
  author = {Veltz, Romain},
  url = {https://hal.archives-ouvertes.fr/hal-02902346},
  institution = {{Inria Sophia-Antipolis}},
  year = {2020},
  month = Jul,
  keywords = {pseudo-arclength-continuation ; periodic-orbits ; floquet ; gpu ; bifurcation-diagram ; deflation ; newton-krylov},
  pdf = {https://hal.archives-ouvertes.fr/hal-02902346/file/354c9fb0d148262405609eed2cb7927818706f1f.tar.gz},
  hal_id = {hal-02902346},
  hal_version = {v1},
  eprint = {hal-02902346},
  eprinttype = {hal},
}

GitHub Events

Total
  • Create event: 34
  • Commit comment event: 29
  • Release event: 15
  • Issues event: 54
  • Watch event: 28
  • Issue comment event: 272
  • Push event: 160
  • Pull request review event: 1
  • Pull request review comment event: 1
  • Pull request event: 47
  • Fork event: 7
Last Year
  • Create event: 34
  • Commit comment event: 29
  • Release event: 15
  • Issues event: 54
  • Watch event: 28
  • Issue comment event: 272
  • Push event: 160
  • Pull request review event: 1
  • Pull request review comment event: 1
  • Pull request event: 47
  • Fork event: 7

Issues and Pull Requests

Last synced: 6 months ago

All Time
  • Total issues: 153
  • Total pull requests: 104
  • Average time to close issues: about 2 months
  • Average time to close pull requests: about 1 month
  • Total issue authors: 62
  • Total pull request authors: 16
  • Average comments per issue: 6.06
  • Average comments per pull request: 1.18
  • Merged pull requests: 38
  • Bot issues: 1
  • Bot pull requests: 77
Past Year
  • Issues: 44
  • Pull requests: 49
  • Average time to close issues: 12 days
  • Average time to close pull requests: 19 days
  • Issue authors: 23
  • Pull request authors: 7
  • Average comments per issue: 5.09
  • Average comments per pull request: 1.37
  • Merged pull requests: 20
  • Bot issues: 1
  • Bot pull requests: 37
View more stats
Top Authors
Issue Authors
  • TorkelE (29)
  • Datseris (11)
  • rveltz (9)
  • yhchang96 (8)
  • rseydam (7)
  • gszep (6)
  • antoine-levitt (6)
  • Azercoco (6)
  • LEquinoxy (3)
  • axla-io (3)
  • RuqiShi12 (3)
  • github-actions[bot] (2)
  • twildi (2)
  • BambOoxX (2)
  • liuyxpp (2)
Pull Request Authors
  • github-actions[bot] (97)
  • BambOoxX (5)
  • danielwe (4)
  • Azercoco (2)
  • Datseris (2)
  • gszep (2)
  • antoine-levitt (2)
  • amontoison (2)
  • gdalle (2)
  • macquarrielucas (2)
  • twildi (2)
  • isaacsas (1)
  • paniash (1)
  • dkarrasch (1)
  • musvaage (1)
Top Labels
Issue Labels
enhancement (14) bug (5) good first issue (2) question (1)
Pull Request Labels

Packages

  • Total packages: 1
  • Total downloads:
    • julia 108 total
  • Total dependent packages: 4
  • Total dependent repositories: 0
  • Total versions: 48
juliahub.com: BifurcationKit

A Julia package to perform Bifurcation Analysis

  • Versions: 48
  • Dependent Packages: 4
  • Dependent Repositories: 0
  • Downloads: 108 Total
Rankings
Dependent repos count: 9.9%
Average: 16.5%
Dependent packages count: 23.0%
Last synced: 6 months ago

Dependencies

.github/workflows/TagBot.yml actions
  • JuliaRegistries/TagBot v1 composite
.github/workflows/ci.yml actions
  • actions/cache v1 composite
  • actions/checkout v2 composite
  • codecov/codecov-action v1 composite
  • julia-actions/julia-buildpkg v1 composite
  • julia-actions/julia-processcoverage v1 composite
  • julia-actions/julia-runtest v1 composite
  • julia-actions/setup-julia v1 composite
.github/workflows/CompatHelper.yml actions