fronts
Numerical library for nonlinear diffusion problems in semi-infinite domains
Science Score: 57.0%
This score indicates how likely this project is to be science-related based on various indicators:
-
✓CITATION.cff file
Found CITATION.cff file -
✓codemeta.json file
Found codemeta.json file -
✓.zenodo.json file
Found .zenodo.json file -
✓DOI references
Found 3 DOI reference(s) in README -
○Academic publication links
-
○Committers with academic emails
-
○Institutional organization owner
-
○JOSS paper metadata
-
○Scientific vocabulary similarity
Low similarity (11.4%) to scientific vocabulary
Keywords
Keywords from Contributors
Repository
Numerical library for nonlinear diffusion problems in semi-infinite domains
Basic Info
- Host: GitHub
- Owner: gerlero
- License: bsd-3-clause
- Language: Python
- Default Branch: main
- Homepage: https://fronts.readthedocs.io
- Size: 1.02 MB
Statistics
- Stars: 5
- Watchers: 3
- Forks: 0
- Open Issues: 1
- Releases: 26
Topics
Metadata Files
README.md
Fronts is a Python numerical library for nonlinear diffusion problems based on the Boltzmann transformation.
```python Python 3.9.6 (default, Sep 26 2022, 11:37:49)
import fronts θ = fronts.solve(D="exp(7*θ)/2", i=0, b=1) # i: initial value, b: boundary value θ(r=10, t=3) 0.9169685387070694 θ.d_dr(10,3) # ∂θ/∂r -0.01108790437249313 print("Welcome to the Fronts project page.") ```
| ⚡️ Fronts is also available as a Julia package. We recommend using the Julia version, particularly where performance is important | | ---- |
Overview
With Fronts, you can effortlessly find solutions to many problems of nonlinear diffusion along a semi-infinite axis r, i.e.:
$$\frac{\partial\theta}{\partial t} = \nabla\cdot\left[D(\theta)\frac{\partial\theta}{\partial r}\mathbf{\hat{r}}\right]$$
where D is a known positive function and θ is an unkown function of r and t.
Fronts includes functionality to solve problems with a Dirichlet boundary condition (start with fronts.solve()), as well as some radial problems with a fixed-flowrate boundary condition (with fronts.solve_flowrate()). In every case, D can be any function defined by the user or obtained from the fronts.D module.
It works by transforming the above nonlinear partial differential equation (PDE) into a more manageable (but still nonlinear) ordinary differential equation (ODE), using a technique known as the Boltzmann transformation, which it then solves with a combination of high-order numerical ODE integration (provided by the SciPy library) and specialized logic.
For this class of problems, you will find that Fronts can be easier to use, faster, and more robust than the classical numerical PDE solvers you would otherwise have to use. Moreover, the solutions found by Fronts are such that their partial derivatives and flux fields are also available in continuous form. Finally, a considerable effort has been made to have Fronts "just work" in practice, with no adjustment of numerical parameters required (in fact, the functions mentioned so far do not even require a starting mesh).
Fronts can also help you solve the inverse problem of finding D when θ is given. Every feature of Fronts is covered in the documentation, and the project includes many example cases (though you may start with the Usage section below).
Fronts is open source and works great with the tools of the SciPy ecosystem.
Why Fronts?
Problems compatible with Fronts appear in many areas of physics. For instance, if we take θ as the water content or saturation and D as the moisture diffusivity, the above equation translates into what is known as the moisture diffusivity equation, which is a special case of the Richards equation that describes capillary flow in porous media. For this application, Fronts even includes implementations of the commonly used models: fronts.D.brooks_and_corey() and fronts.D.van_genuchten().
Of particular interest to the creators of Fronts is the fact that it can be used to model the configuration known as "lateral flow" in the field of paper-based microfluidics. The name "Fronts" is a reference to the wetting fronts that appear under these conditions, the study of which motivated the creation of this software.
Other problems of this class appear in the study of the diffusion of solutions in polymer matrices as well as diffusion problems in solids (e.g. annealing problems in metallurgy).
As mentioned before, if your problem is supported, you can expect Fronts to be easier to use, faster, and more robust than other tools. Try it out!
Installation
Fronts currently runs on Python 3.7 and later.
Install Fronts with pip by running this command in a terminal:
sh
python3 -m pip install fronts
This will download and install the most recent version of Fronts available on PyPI.
Optional: Matplotlib
Running the bundled examples requires the visualization library Matplotlib. This library is not installed automatically with Fronts, so if you don't already have it, you may want to install it manually by running:
sh
python3 -m pip install matplotlib
Optionally, Fronts can be installed in a virtual environment, or the --user option can be added to the previous commands to install the packages for the current user only (which does not require system administrator privileges).
Usage
Let's say we want to solve the following initial-boundary value problem:
Find c such that:
$$ \begin{cases} \dfrac{\partial c}{\partial t} = \dfrac{\partial}{\partial r}\left(c^4\dfrac{\partial c}{\partial r}\right) & r>0,t>0\ c(r,0)=0.1 & r>0\ c(0,t)=1 & t>0\ \end{cases} $$
With Fronts, all it takes is a call to fronts.solve(). The function requires the diffusivity function D, which we pass as an expression so that solve() can get the derivatives it needs by itself (alternatively, in this case we could also have used fronts.D.power_law() to obtain D). Besides D, we only need to pass the initial and boundary values as i and b. The Python code is:
python
import fronts
c = fronts.solve(D="c**4", i=0.1, b=1)
The call to solve() finishes within a fraction of a second. c is assigned a Solution object, which can be called directly but also has some interesting methods such as d_dr(), d_dt() and flux().
We can now plot the solution for arbitrary r and t. For example, with r between 0 and 10 and t=60:
```python import numpy as np import matplotlib.pyplot as plt
r = np.linspace(0, 10, 200) plt.plot(r, c(r, t=60)) plt.xlabel("r") plt.ylabel("c") plt.show() ```
The plot looks like this:
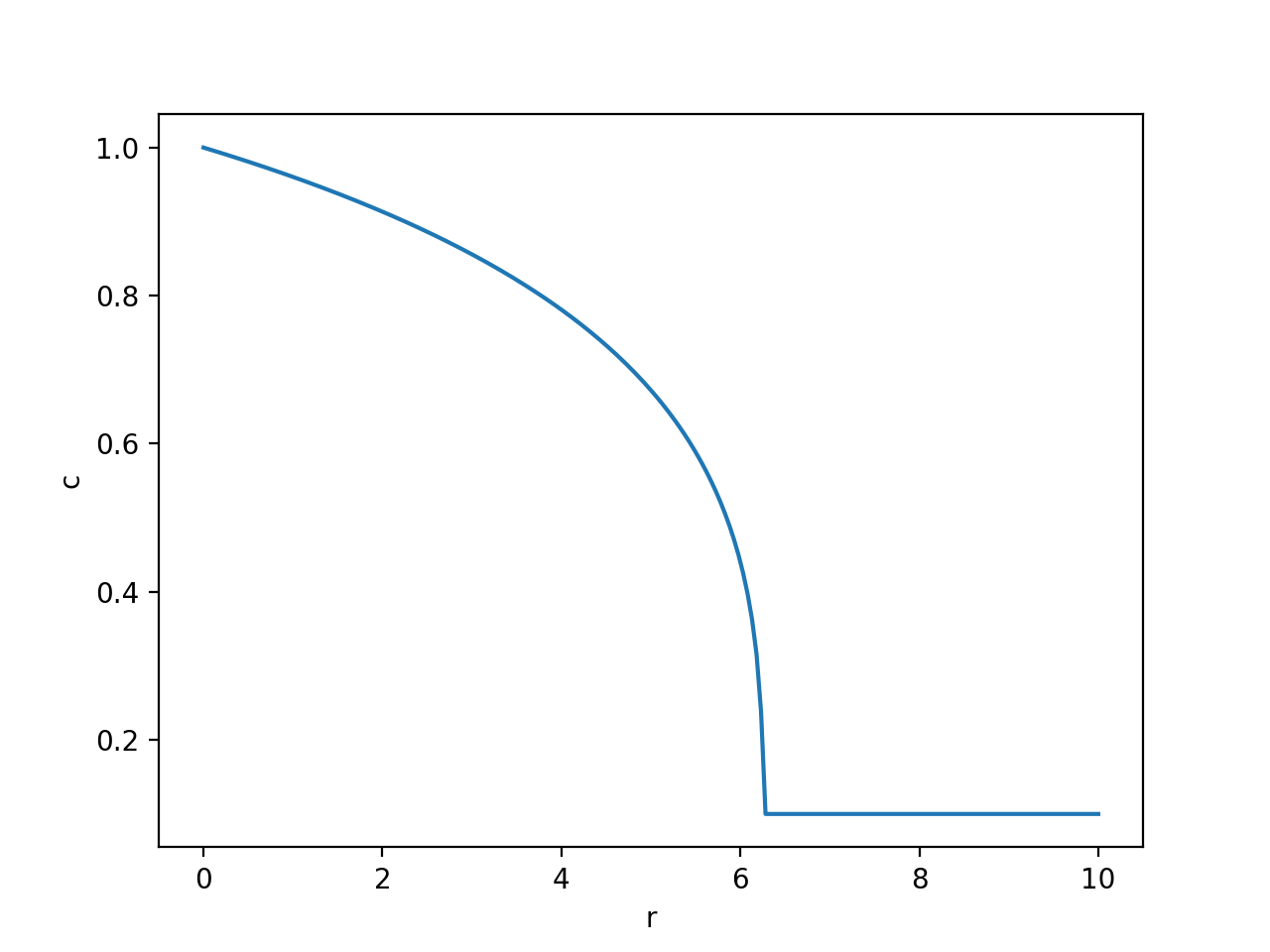
Finally, let us plot the flux at t=60:
python
plt.plot(r, c.flux(r, t=60))
plt.xlabel("r")
plt.ylabel("flux")
plt.show()
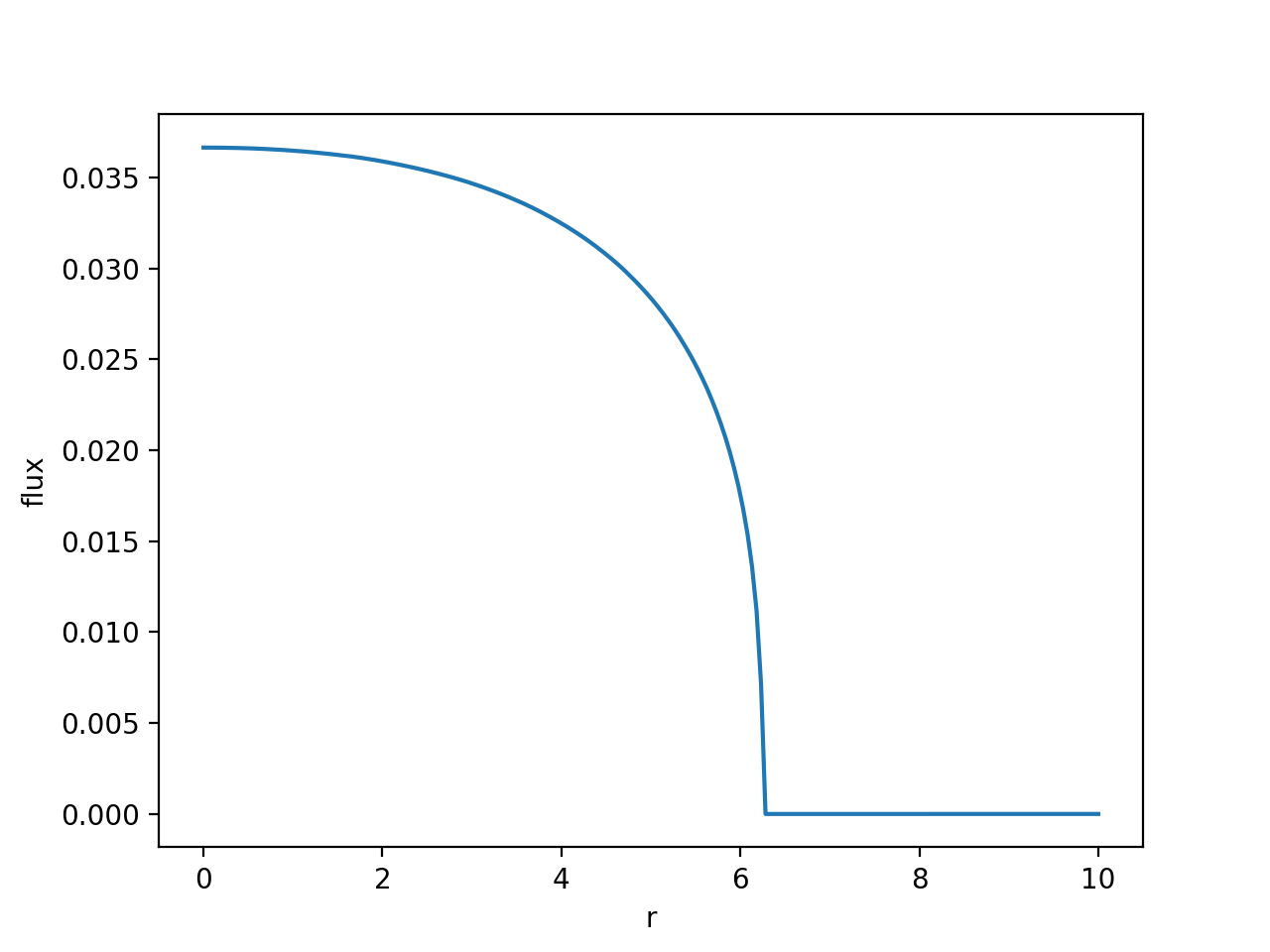
Project links
Authors
- Gabriel S. Gerlero @gerlero
- Pablo A. Kler @pabloakler
- Claudio L. A. Berli
Fronts was conceived and is developed by members of the Santa Fe Microfluidics Group (GSaM) at the Research Center for Computational Methods (CIMEC, UNL-CONICET) and the Institute of Technological Development for the Chemical Industry (INTEC, UNL-CONICET) in Santa Fe, Argentina.
License
Fronts is open-source software available under the BSD 3-clause license.
Owner
- Name: Gabriel Gerlero
- Login: gerlero
- Kind: user
- Location: Santa Fe, Argentina
- Company: @microfluidica
- Repositories: 10
- Profile: https://github.com/gerlero
Information Systems Engineer. PhD candidate in Computational Mechanics at CIMEC. Physics TA at UNL. Santa Fe Microfluidics Group (GSaM).
Citation (CITATION.cff)
cff-version: 1.2.0
preferred-citation:
type: article
authors:
- given-names: Gabriel S.
family-names: Gerlero
- given-names: Claudio L. A.
family-names: Berli
- given-names: Pablo A.
family-names: Kler
title: Open-source high-performance software packages for direct and inverse solving of horizontal capillary flow
journal: Capillarity
year: 2023
volume: 6
issue: 2
start: 31
end: 40
doi: 10.46690/capi.2023.02.02
GitHub Events
Total
- Release event: 4
- Watch event: 1
- Delete event: 21
- Issue comment event: 13
- Push event: 44
- Pull request event: 39
- Create event: 23
Last Year
- Release event: 4
- Watch event: 1
- Delete event: 21
- Issue comment event: 13
- Push event: 44
- Pull request event: 39
- Create event: 23
Committers
Last synced: 10 months ago
Top Committers
| Name | Commits | |
|---|---|---|
| Gabriel Gerlero | g****o | 267 |
| dependabot[bot] | 4****] | 20 |
Issues and Pull Requests
Last synced: 8 months ago
All Time
- Total issues: 3
- Total pull requests: 92
- Average time to close issues: 6 days
- Average time to close pull requests: 4 days
- Total issue authors: 2
- Total pull request authors: 2
- Average comments per issue: 1.33
- Average comments per pull request: 0.78
- Merged pull requests: 91
- Bot issues: 0
- Bot pull requests: 21
Past Year
- Issues: 0
- Pull requests: 23
- Average time to close issues: N/A
- Average time to close pull requests: 7 days
- Issue authors: 0
- Pull request authors: 2
- Average comments per issue: 0
- Average comments per pull request: 0.65
- Merged pull requests: 23
- Bot issues: 0
- Bot pull requests: 8
Top Authors
Issue Authors
- gerlero (3)
- IvanOstr (1)
- dependabot[bot] (1)
Pull Request Authors
- gerlero (88)
- dependabot[bot] (31)
Top Labels
Issue Labels
Pull Request Labels
Packages
- Total packages: 1
-
Total downloads:
- pypi 160 last-month
- Total dependent packages: 0
- Total dependent repositories: 1
- Total versions: 28
- Total maintainers: 1
pypi.org: fronts
Numerical library for nonlinear diffusion problems in semi-infinite domains
- Homepage: https://github.com/gerlero/fronts
- Documentation: https://fronts.readthedocs.io
- License: BSD License
-
Latest release: 1.2.7
published 10 months ago
Rankings
Maintainers (1)
Dependencies
- actions/checkout v3 composite
- actions/setup-python v4 composite
- codecov/codecov-action v3 composite
- actions/checkout v3 composite
- actions/setup-python v4 composite
- battila7/get-version-action v2 composite
- pypa/gh-action-pypi-publish release/v1 composite
- docker/build-push-action v5 composite
- docker/login-action v3 composite
- docker/metadata-action v5 composite
- docker/setup-buildx-action v3 composite
- docker/setup-qemu-action v3 composite
- actions/checkout v4 composite
- peter-evans/dockerhub-description v3 composite
- python 3.12-slim build
- numpy *
- scipy >=1.4.0,<2
- sympy ==1.*










