https://github.com/androsovas/intvalpy
IntvalPy - a Python interval computation library
Science Score: 36.0%
This score indicates how likely this project is to be science-related based on various indicators:
-
○CITATION.cff file
-
✓codemeta.json file
Found codemeta.json file -
✓.zenodo.json file
Found .zenodo.json file -
○DOI references
-
✓Academic publication links
Links to: researchgate.net -
○Committers with academic emails
-
○Institutional organization owner
-
○JOSS paper metadata
-
○Scientific vocabulary similarity
Low similarity (8.8%) to scientific vocabulary
Keywords
Repository
IntvalPy - a Python interval computation library
Basic Info
- Host: GitHub
- Owner: AndrosovAS
- License: mit
- Language: Python
- Default Branch: master
- Homepage: https://intvalpy.readthedocs.io
- Size: 6.43 MB
Statistics
- Stars: 12
- Watchers: 2
- Forks: 3
- Open Issues: 4
- Releases: 2
Topics
Metadata Files
README.md
Interval library in Python
The Python module implements an algebraically closed interval arithmetic for interval computations, solving interval systems of both linear and nonlinear equations, and visualizing solution sets for interval systems of equations.
For details, see the complete documentation on API.
Links
A detailed monograph on interval theory
Installation
Ensure you have all the system-wide dependencies installed, then install the module using pip:
pip install intvalpy
Examples
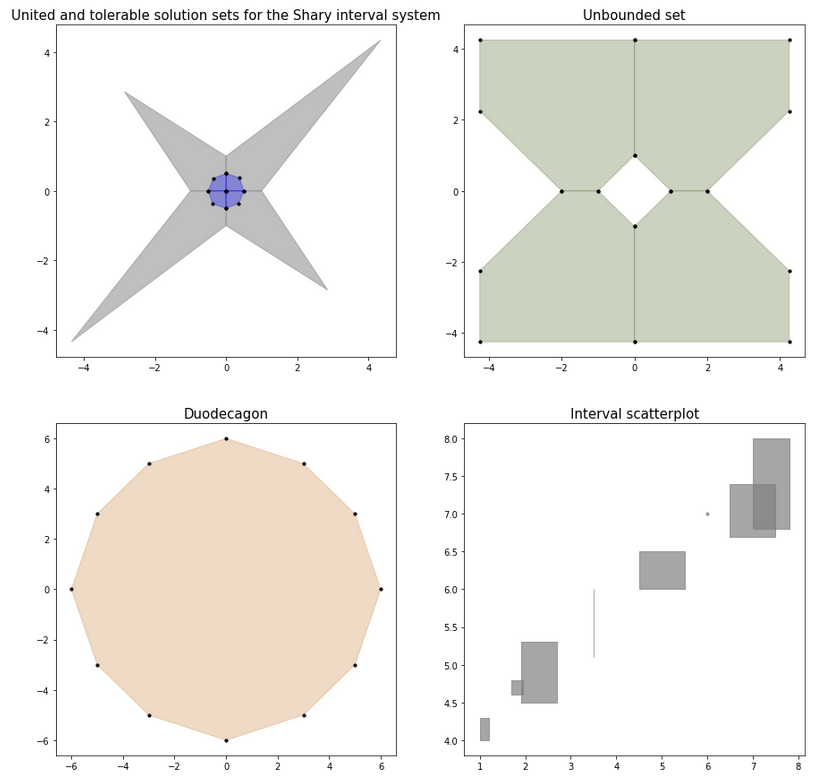
Visualizing solution sets
For a system of linear inequalities of the form A * x >= b or for an interval system of linear algebraic equations A * x = b,
the solution sets are known to be polyhedral sets, convex or non-convex. We can visualize them and display all their vertices:
```python import intvalpy as ip ip.precision.extendedPrecisionQ = False import numpy as np
iplt = ip.IPlot(figsize=(15, 15)) fig, ax = iplt.subplots(nrows=2, ncols=2)
A, b = ip.Shary(2) sharyuni = ip.IntLinIncR2(A, b, show=False) sharytol = ip.IntLinIncR2(A, b, consistency='tol', show=False)
axindex = (0, 0) ax[axindex].settitle('United and tolerable solution sets for the Shary interval system') ax[axindex].title.setsize(15) iplt.IntLinIncR2(sharyuni, color='gray', alpha=0.5, s=0, axindex=axindex) iplt.IntLinIncR2(sharytol, color='blue', alpha=0.3, s=10, axindex=axindex)
A = ip.Interval([ [[-1, 1], [-1, 1]], [[-1, -1], [-1, 1]] ]) b = ip.Interval([[1, 1], [-2, 2]]) unconstrained_set = ip.IntLinIncR2(A, b, show=False)
axindex = (0, 1) ax[axindex].settitle('Unbounded set') ax[axindex].title.setsize(15) iplt.IntLinIncR2(unconstrained_set, color='darkolivegreen', alpha=0.3, s=10, axindex=axindex)
A = -np.array([[-3, -1], [-2, -2], [-1, -3], [1, -3], [2, -2], [3, -1], [3, 1], [2, 2], [1, 3], [-1, 3], [-2, 2], [-3, 1]]) b = -np.array([18,16,18,18,16,18,18,16,18,18,16,18]) duodecagon = ip.lineqs(A, b, show=False)
axindex = (1, 0) ax[axindex].settitle('Duodecagon') ax[axindex].title.setsize(15) iplt.lineqs(duodecagon, color='peru', alpha=0.3, s=10, axindex=axindex)
x = ip.Interval([[1, 1.2], [1.9, 2.7], [1.7, 1.95], [3.5, 3.5], [4.5, 5.5], [6, 6], [6.5, 7.5], [7, 7.8]]) y = ip.Interval([[4, 4.3], [4.5, 5.3], [4.6, 4.8], [5.1, 6], [6, 6.5], [7, 7], [6.7, 7.4], [6.8, 8]])
axindex = (1, 1)
ax[axindex].settitle('Interval scatterplot')
ax[axindex].title.setsize(15)
iplt.scatter(x, y, color='gray', alpha=0.7, s=10, axindex=axindex)
```
It is also possible to create a three-dimensional (or two-dimensional) slice of an N-dimensional figure to visualize the solution set with fixed N-3 (or N-2) parameters. A specific implementation of this algorithm can be found in the examples.
Recognizing functionals:
Before we start solving a system of equations with interval data it is necessary to understand whether it is solvable or not.
To do this we consider the problem of decidability recognition, i.e. non-emptiness of the set of solutions.
In the case of an interval linear (m x n)-system of equations, we will need to solve no more than 2\ :sup:n
linear inequalities of size 2m+n. This follows from the fact of convexity and polyhedra of the intersection of the sets of solutions
interval system of linear algebraic equations (ISLAE) with each of the orthants of R\ :sup:n space.
Reducing the number of inequalities is fundamentally impossible, which follows from the fact that the problem is intractable,
i.e. its NP-hardness. It is clear that the above described method is applicable only for small dimensionality of the problem,
that is why the recognizing functional method was proposed.
After global optimization, if the value of the functional is non-negative, then the system is solvable. If the value is negative, then the set of parameters consistent with the data is empty, but the argument delivering the maximum of the functional minimizes this inconsistency.
As an example, it is proposed to investigate the Bart-Nuding system for the emptiness/non-emptiness of the tolerance set of solutions:
```python import intvalpy as ip
transition from extend precision (type mpf) to double precision (type float)
ip.precision.extendedPrecisionQ = False
A = ip.Interval([ [[2, 4], [-2, 1]], [[-1, 2], [2, 4]] ]) b = ip.Interval([[-2, 2], [-2, 2]])
tol = ip.linear.Tol.maximize( A = A, b = b, x0 = None, weight = None, linear_constraint = None ) print(tol) ```
External decision evaluation:
To obtain an optimal external estimate of the united set of solutions of an interval system linear of algebraic equations (ISLAE), a hybrid method of splitting PSS solutions is implemented. Since the task is NP-hard, the process can be stopped by the number of iterations completed. PSS methods are consistently guaranteeing, i.e. when the process is interrupted at any number of iterations, an approximate estimate of the solution satisfies the required estimation method.
```python import intvalpy as ip
transition from extend precision (type mpf) to double precision (type float)
ip.precision.extendedPrecisionQ = False
A, b = ip.Shary(12, N=12, alpha=0.23, beta=0.35) pss = ip.linear.PSS(A, b) print('pss: ', pss) ```
Interval system of nonlinear equations:
For nonlinear systems, the simplest multidimensional interval methods of Krawczyk and Hansen-Sengupta are implemented for solving nonlinear systems:
```python import intvalpy as ip
transition from extend precision (type mpf) to double precision (type float)
ip.precision.extendedPrecisionQ = False
epsilon = 0.1 def f(x): return ip.asinterval([x[0]2 + x[1]2 - 1 - ip.Interval(-epsilon, epsilon), x[0] - x[1]**2])
def J(x):
result = [[2x[0], 2x[1]],
[1, -2*x[1]]]
return ip.asinterval(result)
ip.nonlinear.HansenSengupta(f, J, ip.Interval([0.5,0.5],[1,1])) ```
The library also provides the simplest interval global optimization:
```python import intvalpy as ip
transition from extend precision (type mpf) to double precision (type float)
ip.precision.extendedPrecisionQ = False
def levy(x): z = 1 + (x - 1) / 4 t1 = np.sin( np.pi * z[0] )*2 t2 = sum(((x - 1) * 2 * (1 + 10 * np.sin(np.pi * x + 1) ** 2))[:-1]) t3 = (z[-1] - 1) ** 2 * (1 + np.sin(2np.pi * z[-1]) * 2) return t1 + t2 + t3
N = 2 x = ip.Interval([-5]N, [5]N) ip.nonlinear.globopt(levy, x, tol=1e-14) ```
Owner
- Name: Artem Androsov
- Login: AndrosovAS
- Kind: user
- Location: Russia, Novosibirsk
- Website: artem.androsov@gmail.com
- Repositories: 2
- Profile: https://github.com/AndrosovAS
GitHub Events
Total
- Watch event: 3
- Push event: 6
Last Year
- Watch event: 3
- Push event: 6
Committers
Last synced: almost 3 years ago
All Time
- Total Commits: 135
- Total Committers: 4
- Avg Commits per committer: 33.75
- Development Distribution Score (DDS): 0.526
Top Committers
| Name | Commits | |
|---|---|---|
| Artem Androsov | 6****S@u****m | 64 |
| Maestross | 6****s@u****m | 47 |
| Sergey P. Shary | 7****y@u****m | 17 |
| AndrosovAS | a****v@g****m | 7 |
Issues and Pull Requests
Last synced: 8 months ago
All Time
- Total issues: 17
- Total pull requests: 15
- Average time to close issues: 3 months
- Average time to close pull requests: about 2 hours
- Total issue authors: 4
- Total pull request authors: 2
- Average comments per issue: 1.24
- Average comments per pull request: 0.0
- Merged pull requests: 14
- Bot issues: 0
- Bot pull requests: 0
Past Year
- Issues: 1
- Pull requests: 0
- Average time to close issues: N/A
- Average time to close pull requests: N/A
- Issue authors: 1
- Pull request authors: 0
- Average comments per issue: 0.0
- Average comments per pull request: 0
- Merged pull requests: 0
- Bot issues: 0
- Bot pull requests: 0
Top Authors
Issue Authors
- AndrosovAS (9)
- mvnayagam (2)
- realkarmakun (1)
- Katalien (1)
Pull Request Authors
- AndrosovAS (12)
- ZvyaginMA (2)
Top Labels
Issue Labels
Pull Request Labels
Packages
- Total packages: 2
-
Total downloads:
- pypi 175 last-month
-
Total dependent packages: 1
(may contain duplicates) -
Total dependent repositories: 1
(may contain duplicates) - Total versions: 35
- Total maintainers: 1
pypi.org: intvalpy-test
An interval library in Python that uses classical interval arithmetic and Kauher arithmetic + Kahan division in some functions
- Homepage: https://github.com/AndrosovAS/intvalpy
- Documentation: https://intvalpy-test.readthedocs.io/
- License: MIT License
-
Latest release: 0.0.13
published over 4 years ago
Rankings
pypi.org: intvalpy
IntvalPy - a Python interval computation library
- Homepage: https://github.com/AndrosovAS/intvalpy
- Documentation: https://intvalpy.readthedocs.io/
- License: MIT License
-
Latest release: 1.6.6
published 9 months ago