Reyna: A minimal overhead polytopal discontinuous Galerkin finite element library
Reyna: A minimal overhead polytopal discontinuous Galerkin finite element library - Published in JOSS (2026)
Science Score: 87.0%
This score indicates how likely this project is to be science-related based on various indicators:
-
○CITATION.cff file
-
○codemeta.json file
-
○.zenodo.json file
-
✓DOI references
Found 1 DOI reference(s) in JOSS metadata -
○Academic publication links
-
○Committers with academic emails
-
○Institutional organization owner
-
✓JOSS paper metadata
Published in Journal of Open Source Software
Repository
A lightweight polytopal discontinuous Galerkin finite element library.
Basic Info
- Host: GitHub
- Owner: mattevs24
- License: mit
- Language: Python
- Default Branch: main
- Homepage: https://reyna.readthedocs.io/en/latest/
- Size: 4.36 MB
Statistics
- Stars: 0
- Watchers: 1
- Forks: 2
- Open Issues: 0
- Releases: 3
Metadata Files
README.md
reyna
A lightweight Python package for solving partial differential equations (PDEs) using polygonal discontinuous Galerkin finite elements, providing a flexible and efficient way to approximate solutions to complex PDEs.
Features
- Support for various polygonal element types (e.g., triangles, quadrilaterals, etc.)
- Easy-to-use API for mesh generation, assembly, and solving PDEs.
- High performance with optimized solvers for large-scale problems.
- Supports linear advection-diffusion-reaction equations.
- Extensible framework: easily integrate custom element types, solvers, or boundary conditions.
Installation
You can install the package via pip. First, clone the repository and then install it using pip:
Install from PyPI:
shell
pip install reyna
Install from source:
shell
pip install git+https://github.com/mattevs24/reyna.git
Please use a Python version 3.8-<3.12 to ensure that all features work as expected.
Example Usage
Create a Simple Mesh
A simple example to begin with is the RectangleDomain object. This requires just the bounding
box as an input. In this case, we consider the unit square; $[0, 1]^2$. We then use poly_mesher
to generate a bounded Voronoi mesh of the domain. This uses Lloyd's algorithm, which can produce
edges that are machine precision in length. To avoid this for benchmarking and other critical
purposes, use the cleaned keyword, set to True.
```python import numpy as np
from reyna.polymesher.twodimensional.domains import RectangleDomain from reyna.polymesher.twodimensional.main import poly_mesher
domain = RectangleDomain(boundingbox=np.array([[0, 1], [0, 1]])) polymesh = polymesher(domain, maxiterations=10, n_points=1024) ```
Generating the Geometry Information
The DGFEM code requires additional information about the mesh to be able to run, including which edges
are boundary edges and their corresponding normals as well as information on a given subtriagulation to
be able to numerically integrate with the required precision. This is done using the DGFEMgeometry function.
```python from reyna.geometry.two_dimensional.DGFEM import DGFEMGeometry
geometry = DGFEMGeometry(poly_mesh) ```
Defining the Partial Differential Equation
To define the PDE, we need to call the DGFEM object. We then add data in the form of the general coefficients for a (up-to) second order PDE of the form
$$ -\nabla\cdot(a\nabla u) + b\cdot\nabla u + cu = f $$
where $a$ is the diffusion tensor, $b$ is the advection vector, $c$ is the reation functional and $f$ is the forcing functional. All of these functions must be able to take in a (N, 2) array of points and output tensors of the correct shape; (N, 2, 2), (N, 2), (N,) and (N,) respectively. An example is given
```python def diffusion(x): out = np.zeros((x.shape[0], 2, 2), dtype=np.float64) for i in range(x.shape[0]): out[i, 0, 0] = 1.0 out[i, 1, 1] = 1.0 return out
advection = lambda x: np.ones(x.shape, dtype=float) reaction = lambda x: np.pi ** 2 * np.ones(x.shape[0], dtype=float) forcing = lambda x: np.pi * (np.cos(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1]) + np.sin(np.pi * x[:, 0]) * np.cos(np.pi * x[:, 1])) + \ 3.0 * np.pi ** 2 * np.sin(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1])
solution = lambda x: np.sin(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1]) ```
We use the solution function here as the boundary conditions for the solver.
Adding data and Assembly
We can now call the solver, add the data and assemble.
```python
from reyna.DGFEM.two_dimensional.main import DGFEM
dg = DGFEM(geometry, polynomial_degree=1)
dg.adddata( diffusion=diffusion, advection=advection, reaction=reaction, dirichletbcs=solution, forcing=forcing )
dg.dgfem(solve=True) ```
Setting the solve input to True generates the solution vector. If this is False, just the
stiffness matrix and data vector are generated.
Visualize the solution
We also have a method to plot the data, plot_DG, but this is limited to polynomial degree 1
with limited support for polynomial degree 0. See the example below
python
dg.plot_DG()
or for more customisation, use the function plot_DG,
```python from reyna.DGFEM.twodimensional.tools import plotDG
plot_DG(dg.solution, geometry, dg.polydegree) ```
For the given example, we have the solution plot
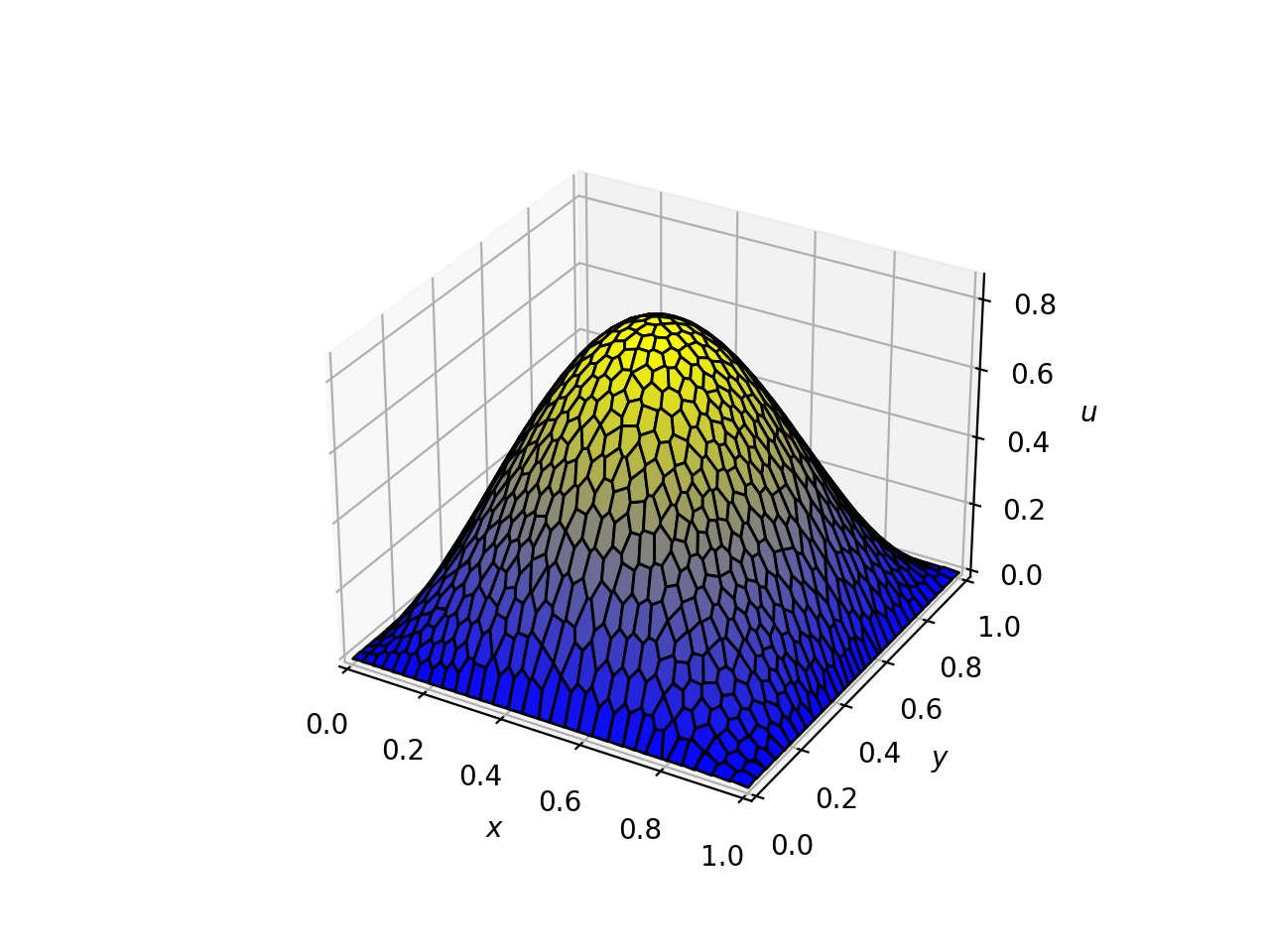
Benchmarking
We have a benchmarking file that may be run availible in the main DGFEM directory. But we also provide an example of the code to be able to calculate yourself
```python
def gradsolution(x: np.ndarray): ux = np.pi * np.cos(np.pi * x[:, 0]) * np.sin(np.pi * x[:, 1]) u_y = np.pi * np.sin(np.pi * x[:, 0]) * np.cos(np.pi * x[:, 1])
return np.vstack((u_x, u_y)).T
dgerror, l2error, h1error = dg.errors( exactsolution=solution, divadvection=lambda x: np.zeros(x.shape[0]), gradexactsolution=gradsolution ) ```
Often, the error rate is calcuated against the maximal cell diameter; the code for this is included in
the DGFEM class under the h method as well as the DGFEMgeometry class under the h method (DGFEMgeometry
additionally contains all the local values of h across the mesh).
python
h = dg.h
h = geometry.h
Note that in a purely advection/diffusion problem, some of the norms are unavailable and return
a None value.
A more advanced Domain Example
There are many predefined domains in the reyna/polymesher/two_dimensional/domains folder including this
more advanced CircleCircleDomain() domain;
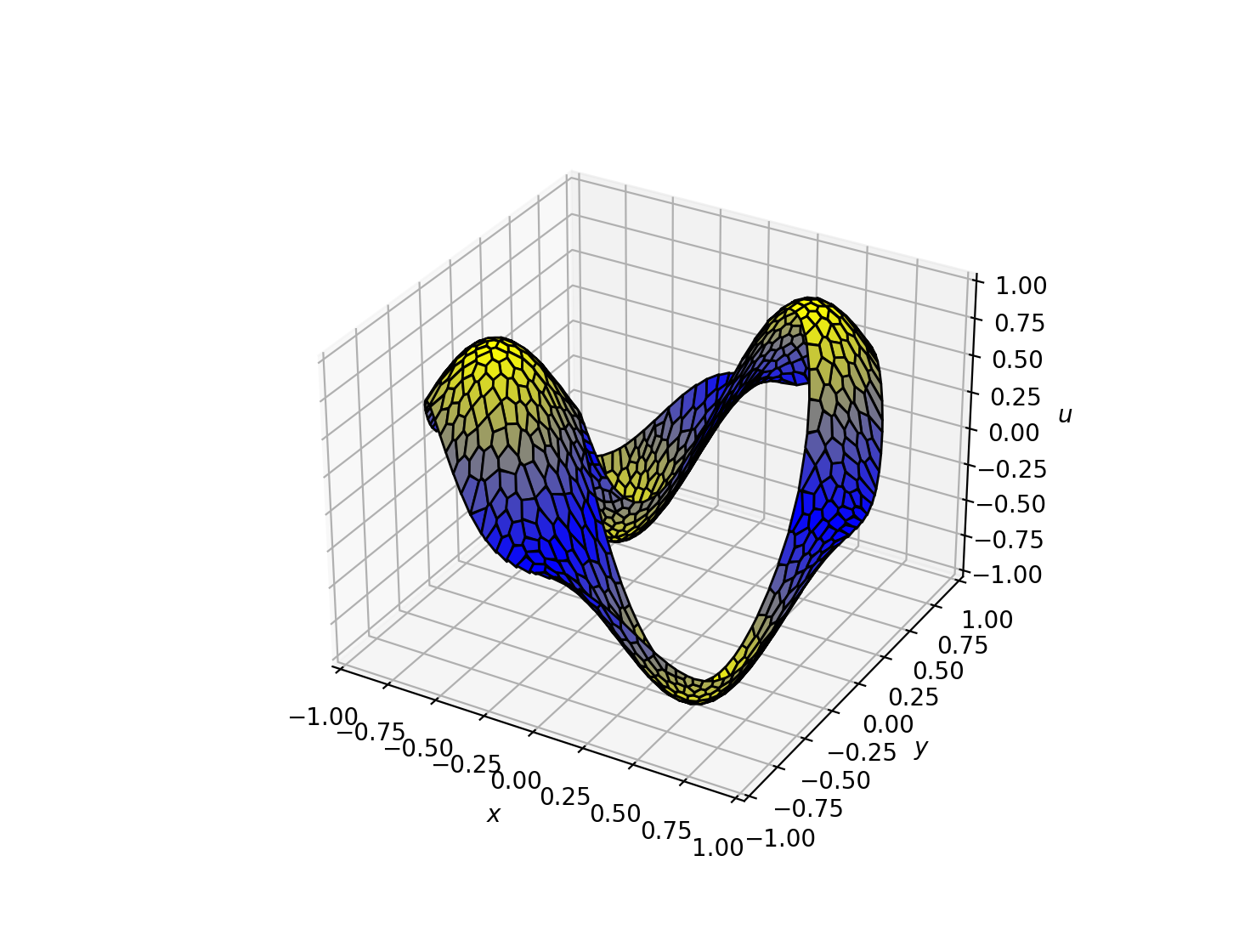
Example Notebooks
There are Jupyter notebooks availible in the GitHub repository which run through several examples of this package in action. This also runs through examples of benchmarking and custom domain generation.
Documentation
For detailed usage and API documentation, please visit our (soon to be) readthedocs. The above example and notebooks cover most cases and the current docstrings are very thorough.
Contributing
This project accepts contributions - see the CONTRIBUTING.md file for details.
License
This project is licensed under the MIT License - see the LICENSE.md file for details.
Credits & Acknowledgements
This package was developed by mattevs24 during a PhD programme funded by the French Alternative Energies and Atomic Energy Commission. A Special thanks to the support of Ansar Calloo, Fraçois Madiot throughout the PhD so far. A further thank you to my interal supervisors Tristan Pryer and Luca Zanetti for their role in this project too and useful feedback on usability and support. Finally, a thank you to Reyna who puts up with all this nonsense!
Upcoming Updates
There are many features that remain to add to this code! We hope to add support for the following features
- Neumann and Robin boundary conditions: further support for more advanced boundary conditions that fit naturally into the DGFEM formulation.
- Mixed boundary conditions: support for multiple types of boundary conditions on the same domain.
- 3D DGFEM: implement a full three dimensional version of the code able to support the same functionality.
Owner
- Name: Matthew Evans
- Login: mattevs24
- Kind: user
- Repositories: 3
- Profile: https://github.com/mattevs24
JOSS Publication
Reyna: A minimal overhead polytopal discontinuous Galerkin finite element library
Authors
Tags
Discontinuous Galerkin Finite Elements Polygonal PolytopalGitHub Events
Total
- Release event: 2
- Delete event: 2
- Member event: 1
- Issues event: 1
- Issue comment event: 2
- Push event: 24
- Public event: 1
- Create event: 5
Last Year
- Release event: 2
- Delete event: 2
- Member event: 1
- Issues event: 1
- Issue comment event: 2
- Push event: 24
- Public event: 1
- Create event: 5
Committers
Last synced: 5 months ago
Top Committers
| Name | Commits | |
|---|---|---|
| Matthew Evans | m****1@g****m | 42 |
| Matthew Evans | 9****4@u****m | 1 |
Issues and Pull Requests
Last synced: 2 months ago
All Time
- Total issues: 0
- Total pull requests: 0
- Average time to close issues: N/A
- Average time to close pull requests: N/A
- Total issue authors: 0
- Total pull request authors: 0
- Average comments per issue: 0
- Average comments per pull request: 0
- Merged pull requests: 0
- Bot issues: 0
- Bot pull requests: 0
Past Year
- Issues: 0
- Pull requests: 0
- Average time to close issues: N/A
- Average time to close pull requests: N/A
- Issue authors: 0
- Pull request authors: 0
- Average comments per issue: 0
- Average comments per pull request: 0
- Merged pull requests: 0
- Bot issues: 0
- Bot pull requests: 0
Top Authors
Issue Authors
Pull Request Authors
Top Labels
Issue Labels
Pull Request Labels
Packages
- Total packages: 1
-
Total downloads:
- pypi 23 last-month
- Total dependent packages: 0
- Total dependent repositories: 0
- Total versions: 4
- Total maintainers: 1
pypi.org: reyna
A minimal overhead, vectorised, polygonal discontinuous Galerkin finite element library.
- Documentation: https://reyna.readthedocs.io/
- License: MIT License Copyright (c) 2025 Matthew Evans Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the "Software"), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions: The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software. THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
-
Latest release: 1.3.0
published 6 months ago
Rankings
Maintainers (1)
Dependencies
- matplotlib >=3.4.0
- numpy >=1.18.0
- scipy >=1.4.0
- shapely >=2.0.0
- matplotlib *
- numpy *
- scipy *
- shapely *




